Exercícios sobre circuitos mistos (com respostas explicadas)
Os exercícios a seguir foram elaborados para ajudar você a compreender, de forma prática e objetiva, como funcionam os circuitos elétricos mistos, que combinam ligações em série e em paralelo.
Cada questão explora situações próximas do cotidiano e inclui respostas explicadas passo a passo, permitindo revisar conceitos fundamentais, aplicar a Lei de Ohm e entender a distribuição de correntes, tensões e resistências em diferentes configurações elétricas.
Questão 1
Em um pequeno laboratório de física, os estudantes montaram um protótipo de painel de iluminação portátil alimentado por uma bateria de 12 V.
No circuito, existe um resistor R1 de 10 Ω em série com dois resistores (R2 de 20 Ω e R3 de 30 Ω) ligados em paralelo, conforme diagrama abaixo:
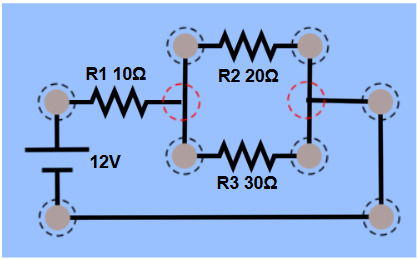
Considerando fios e bateria ideais, determine a corrente que passa pelo resistor R3.
a) 0,18 A
b) 0,20 A
c) 0,22 A
d) 0,24 A
Resposta correta: alternativa c) 0,22 A.
Vamos resolver a questão em cinco passos.
Passo 1: Cálculo da resistência equivalente do paralelo (R2 // R3).
Lembre que para associações em paralelo, temos:
Passo 2: Cálculo da resistência total do circuito.
A resistência R1 está em série com resistência em paralelo. Assim, a resistência total do circuito é dada pela soma de ambas, ou:
Rtotal = R1 + Rpar = 10 + 12 = 22 Ω
Passo 3: Cálculo da corrente total fornecida pela bateria.
Tendo a tensão da bateria e a resistência total, podemos determinar a corrente total usando a Lei de Ohm:
itotal = Vbateria / Rtotal = 12 V / 22 Ω ≃ 0,545 A
Passo 4: Tensão sobre o grupo em paralelo.
Podemos agora determinar a queda de tensão sobre Rpar:
Vpar = itotal . Rpar = 0,545 A . 12 Ω ≃ 6,54 V
Passo 5: Corrente em R3.
Por fim, podemos aplicar a Lei de Ohm no resistor R3 para determinar a corrente que o atravessa:
i3 = Vpar / R3 = 6,54 V / 30 Ω ≃ 0,218 A
Arredondando para dois algarismos significativos ficamos com i3 ≃ 0,22 A.
Questão 2
Em um kit de lanternas de emergência alimentado por uma bateria de 40 V, o circuito de controle de corrente é montado da seguinte forma:
- primeiro um resistor R1 = 10 Ω em série;
- depois dois ramos em paralelo, cada um simulando um conjunto de LEDs (R2 = 20 Ω e R3 = 20 Ω); e,
- por fim, um resistor R4 = 10 Ω em série.
O esquema é:
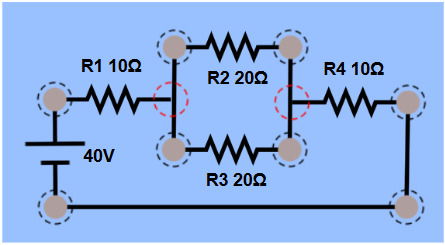
Determine a corrente que passa pelo resistor R3.
a) 0,67 A
b) 1,00 A
c) 1,33 A
d) 1,67 A
Resposta correta: alternativa a) 0,67 A.
Vamos resolver a questão em sete passos.
Passo 1: Cálculo da resistência equivalente do paralelo (R2 // R3).
Para resistências associadas em paralelo, a resistência total é igual à soma dos inversos, ou:
Passo 2: Cálculo da resistência total do circuito.
Agora temos no circuito as resistências R1, Req,par e R4 associadas em série. A resistência total é dada, então, pela soma delas:
Rtotal = R1 + Req,par + R4 = 10 + 10 + 10 = 30 Ω
Passo 3: Cálculo da corrente total fornecida pela bateria.
Tendo a tensão da bateria e a resistência total do circuito, podemos determinar a corrente usando a Lei de Ohm:
itotal = Vbateria / Rtotal = 40 V / 30 Ω ≃ 1,333 A
Passo 4: Determinação da queda de tensão em R1.
Conhecendo a resistência R1 e a corrente que a atravessa, podemos determinar sua tensão ou VR1 usando a Lei de Ohm:
VR1 = itotal . R1 = 1,333 A . 10 Ω = 13,333 V
Passo 5: Queda de tensão em R4.
Da mesma forma podemos determinar a queda de tensão em R4:
VR4 = itotal . R4 = 1,333 A . 10 Ω = 13,333 V
Passo 6: Tensão que aparece nos dois ramos em paralelo.
A tensão no trecho paralelo do circuito é igual à tensão que sobra após as quedas de tensão nas resistências R1 e R4, ou:
Vpar = Vbateria – VR1 – VR4
Vpar = 40 V – 13,333 V – 13,333 V ≃ 13,334 V
Passo 7: Corrente em R3.
Por fim, podemos determinar a corrente que atravessa a resistência R3, visto que conhecemos a tensão à qual eela está submentida. Aplicando a Lei de Ohm em R3:
iR3 = Vpar / R3 = 13,334 V / 20 Ω ≃ 0,667 A
Arredondando para dois algarismos significativos, ficamos com iR3 ≃ 0,67 A.
Questão 3
Em um protótipo de aquecedor elétrico portátil alimentado por uma fonte de 30 V, o circuito é montado da seguinte forma:
- um resistor R1 = 6 Ω em série;
- depois dois ramos em paralelo ⇒ o primeiro ramo tem um único resistor R2 = 9 Ω; e o segundo ramo é uma associação em série de R3 = 6 Ω e R4 = 3 Ω.
O esquema elétrico é:
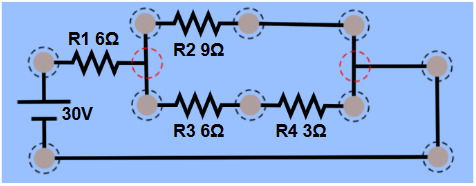
Determine a corrente que passa pelo resistor R1.
a) 1,30 A
b) 1,33 A
c) 1,40 A
d) 1,43 A
Resposta correta: alternativa d) 1,43 A.
Vamos resolver a questão em seis passos.
Passo 1: Resistência do ramo em série (R3 + R4).
Quando as resistências estão em série a resistência total é dada pela soma. Assim:
R34 = R3 + R4 = 6 Ω + 3 Ω = 9 Ω
Passo 2: Resistência equivalente dos ramos em paralelo (R2 // [R3+R4]).
Nesse caso as resistências R2 e R34 estão em paralelo, e a resistência equivalente é dada pela soma dos inversos ou:
Passo 3: Resistência total do circuito.
Agora as resistências R1 e Req,par estão em série e a resistência total do circuito é dada pela soma. Assim:
Rtotal = R1 + Req,par
Rtotal = 6 Ω + 4,5 Ω = 10,5 Ω
Passo 4: Corrente total fornecida pela fonte.
Tendo a tensão da fonte a a resistência total do circuito, podemos determinar a corrente total fornecida usando a Lei de Ohm:
itotal = V / Rtotal
itotal = 30 V / 10,5 Ω ≃ 2,857 A
Passo 5: Queda de tensão sobre o bloco em paralelo.
Sabendo a resistência do bloco paralela e a corrente que o atravessa, podemos determinar a tensão do bloco usando a Lei de Ohm:
Vpar = itotal . Req,par
Vpar ≃ 2,857 A . 4,5 Ω ≃ 12,857 V
Passo 6: Corrente no ramo de R3 e R4 .
Lembre que a corrente nessas duas resistências é a mesma, pois elas estão em série. Aplicando novamente a Lei de Ohm, temos:
iramo = Vpar / (R3 + R4)
iramo ≃ 12,857 V / 9 Ω ≃ 1,429 A
Arredondando para dois algarismos relevantes, ficamos com i3 ≃ 1,43 A.
Questão 4
Em um protótipo de régua de tomadas com proteção por fusível, alimentado por uma fonte de 60 V CC, o circuito de detecção de sobrecarga é composto por um resistor de fusível R1 = 5 Ω em série com três ramos em paralelo, cada um simulando uma “carga”:
- Carga A: R2 = 10 Ω
- Carga B: R3 = 20 Ω
- Carga C: dois resistores em série R4 = 15 Ω e R5 = 15 Ω
O circuito pode ser esquematizado como:
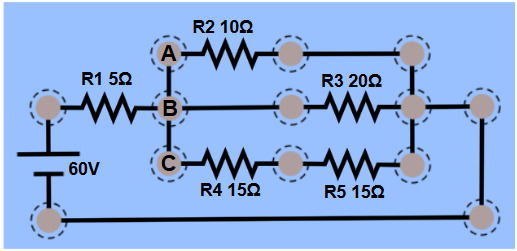
Determine a corrente que passa pelo resistor R2.
a) 1,30 A
b) 1,45 A
c) 1,56 A
d) 5,74 A
Resposta correta: alternativa c) 1,56 A.
Vamos resolver a questão em seis passos.
Passo 1: Resistência da carga C.
Essa carga possui dois resistores em série, R4+R5. A resistência total nesse trecho é dado pela soma delas. Assim:
RC = R4 + R5 = 15 + 15 = 30 Ω
Passo 2: Resistência equivalente dos três ramos em paralelo (R2 // R3 // R_C).
Quando as resistências estão associadas em paralelo, a resistência equivalente é dada pela soma dos inversos:
Passo 3: Resistência total do circuito.
Sabendo a resistência equivalente dos três ramos em paralelo, podemos determinar a resistência total do sistema, pois ela está em série com R1:
Rtotal = R1 + Req,par
Rtotal = 5 + 5,4545 = 10,4545 Ω
Passo 4: Corrente total fornecida pela fonte.
Tendo a resistência total do circuito e o valor da tensão fonte, podemos determinar a corrente total fornecida pela fonte usando a Lei de Ohm:
itotal = V / Rtotal
itotal = 60 V / 10,4545 Ω ≃ 5,7407 A
Passo 5: Tensão sobre o bloco em paralelo.
Sabendo a corrente do sistema e a resistência equivalente nos três ramos paralelos, podemos determinar a tensão no bloco usando a Lei de Ohm:
Vpar = itotal . Req,par
Vpar ≃ 5,7407 A . 5,4545 Ω ≃ 31,30 V
Passo 6: Corrente no resistor R3.
Por fim, conhecendo a tensão e a resistência R3, podemos determinar a corrente que a atravessa usando a Lei de Ohm:
i3 = Vpar / R3
i3 ≃ 31,30 V / 20 Ω ≃ 1,565 A
Arredondando para dois algarismos significativos, ficamos com i3 ≃ 1,56 A.
Questão 5
Lucas, um entusiasta de aeromodelismo, está montando um drone do tipo quadricóptero.
A eletrônica do drone é alimentada por uma bateria de Lítio-Polímero (LiPo) que fornece uma tensão constante de 11,1 V.
O circuito principal pode ser simplificado da seguinte maneira:
A Placa Controladora de Voo (PCV), que gerencia todos os componentes, possui uma resistência interna de 0,5 Ω e está ligada em série com o conjunto de motores.
Os quatro motores do drone são idênticos e estão conectados em paralelo entre si.
Para fins de cálculo, cada motor pode ser considerado um resistor ôhmico. As especificações de cada motor indicam que sua resistência foi projetada para operar idealmente com 22 W de potência quando submetido a uma tensão de 10 V.
O esquema simplificado do circuito é:
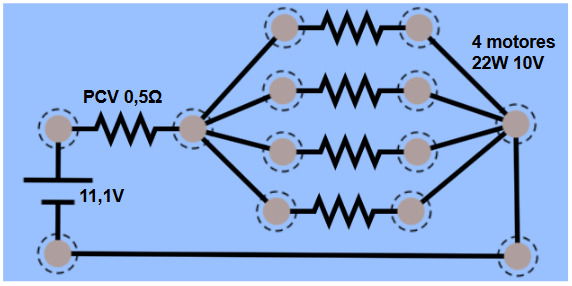
Considerando o drone em pleno funcionamento, qual é a tensão (diferença de potencial) aproximada nos terminais de um dos motores?
a) 2,8 V
b) 7,7 V
c) 9,9 V
d) 10,0 V
Resposta correta: alternativa b) 7,7 V.
O objetivo da questão é encontrar a tensão sobre um dos motores, pois como os quatro motores estão em paralelo, a tensão sobre cada um deles é a mesma.
Essa tensão é a da associação em paralelo (Vparalelo). Para encontrá-la, precisamos primeiro descobrir a corrente total do circuito (itotal).
Vamos fazer isso em cinco passos.
Passo 1: Cálculo da resistência de um único motor (Rmotor).
Utilizamos os dados nominais do motor (22 W e 10 V) e a fórmula da potência P = V² / R. Substituindo os valores, ficamos com:
Rmotor = V2nominal / Pnominal
Rmotor = (10 V)² / 22 W
Rmotor = 100 / 22
Rmotor ≈ 4,55 Ω
Passo 2: Cálculo da resistência equivalente da associação em paralelo dos quatro motores (Rp).
Como os quatro motores são idênticos e estão em paralelo, a resistência equivalente é a resistência de um deles dividida por quatro.
Rp = Rmotor / 4
Rp = 4,55 / 4
Rp ≈ 1,14 Ω
Passo 3: Cálculo da resistência equivalente total do circuito (Req).
A resistência da Placa Controladora de Voo (RPCV) está em série com a resistência equivalente dos motores (Rp). Assim, a resistência equivalente é a soma das duas ou:
Req = RPCV + Rp
Req = 0,5 Ω + 1,14 Ω
Req ≈ 1,64 Ω
Passo 4: Cálculo da corrente total que sai da bateria (itotal).
Usamos a Primeira Lei de Ohm (V = R . i) para o circuito completo, com a tensão da bateria e a resistência equivalente total. Isolando i na equação de Ohm, temos:
itotal = Vbateria / Req
itotal = 11,1 V / 1,64 Ω
itotal ≈ 6,78 A
Passo 5: Cálculo da tensão sobre o conjunto de motores (Vparalelo).
Esta é a tensão que queremos encontrar. Ela pode ser calculada de duas formas,a saber:
Método 1: Usando a Lei de Ohm no trecho em paralelo.
A tensão no trecho paralelo é o produto da corrente total pela resistência equivalente do paralelo, ou:
Vparalelo = itotal . Rp
Vparalelo ≈ 6,78 A . 1,14 Ω
Vparalelo ≈ 7,73 V
Método 2: Subtraindo a queda de tensão na PCV.
Primeiro, calculamos a queda de tensão na resistência em série (VPCV).
VPCV = itotal . RPCV
VPCV ≈ 6,78 A . 0,5 Ω
VPCV ≈ 3,39 V
A tensão que "sobra" para os motores é a tensão da bateria menos essa queda, igual a:
Vparalelo = Vbateria - VPCV
Vparalelo ≈ 11,1 V - 3,39 V
Vparalelo ≈ 7,71 V
Observe que ambos os métodos levam ao mesmo resultado aproximado.
Assim, temos que a tensão nos terminais de cada motor é de aproximadamente 7,7 V.
Questão 6
João está projetando um sistema de iluminação de emergência para um corredor de museu.
O circuito é alimentado por uma bateria de 18 V e inclui um resistor de proteção Rp=3 Ω que fica em série com todo o conjunto.
Em seguida, esse conjunto alimenta duas “ramificações” em paralelo:
- Ramificação A: duas lâmpadas idênticas L1 e L2, cada uma com resistência igual a R1 = R2 = 6 Ω, ligadas em série entre si.
- Ramificação B: uma lâmpada L3, de resistência R3 = 12 Ω.
Diagrama esquemático do circuito:
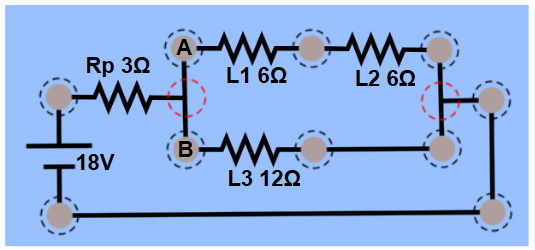
Qual é a intensidade da corrente elétrica que atravessa a lâmpada L1?
a) 0,5 A
b) 0,6 A
c) 0,8 A
d) 1,0 A
Resposta correta: alternativa d) 1,0 A.
Vamos resolver essa questão em 5 passos.
Passo 1: Cálculo da resistência equivalente das ramificações em paralelo:
– Ramificação A, duas lâmpadas em série: RA = R1 + R2 = 6 + 6 = 12 Ω
– Ramificação B, uma única lâmpada: R3 = 12 Ω
As ramificações A e B estão em paralelo. Assim a resistência total do conjunto é dado por:
Passo 2: Cálculo da resistência total do circuito ou RC.
Observe que o resistor de prroteção está em série com o conjunto. Então:
Rcircuito = Rprot + Rp = 3 + 6 = 9 Ω
Passo 3: Podemos determinar a corrente total fornecida pela bateria, usando
i = V / R
itot = 18 V / 9 Ω = 2 A
Passo 4: A queda de tensão no conjunto paralelo fica:
Vpar = Itot . Rparalela = 2 . 6 = 12 V
Passo 5: Por fim, a corrente na ramificação A, que posssui as duas lâmpadas em série com R1 e R2, fica:
iA = Vpar / 12 = 1 A
Como R1 e R2 estão em série, as duas lâmpadas são atravessadas pela mesma corrente de valor 1 A.
Questão 7
Uma estudante de design, está montando seu novo home office.
Para conectar seus equipamentos, ela utiliza uma régua de tomadas (filtro de linha) ligada a uma tomada de 127 V.
A própria régua possui uma fiação interna com uma resistência de 1,0 Ω, que atua em série com os aparelhos nela conectados.
Em sua régua, ela conecta dois equipamentos essenciais, que ficam em paralelo entre si:
- Um carregador de notebook com especificações nominais de 90 W - 120 V.
- Uma luminária de LED com especificações nominais de 30 W - 120 V.
O esquema do circuito formado pode ser representado da seguinte forma:
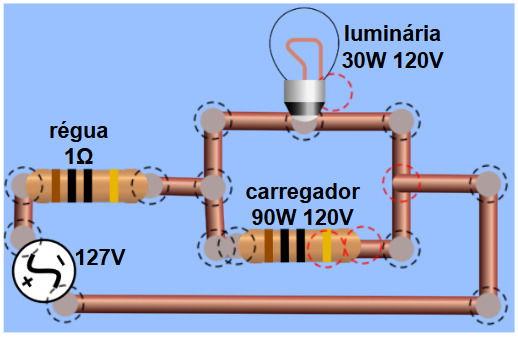
Considere que a resistência dos aparelhos é ôhmica e constante, calculada a partir de suas especificações nominais.
Sabendo que o aquecimento da régua de tomadas é causado pela dissipação de energia em sua resistência interna (efeito Joule), qual é, aproximadamente, a potência dissipada pela fiação interna da régua de tomadas quando ambos os aparelhos estão ligados e funcionando?
a) 0,64 W
b) 98,5 W
c) 1,10 W
d) 120,0 W
Resposta correta: alternativa c) 1,10 W.
Temos que calcular a potência dissipada pela resistência da régua ou Prégua. A fórmula da potência é P = R . i². Portanto, precisamos encontrar a corrente total ou itotal que passa pela régua.
Vamos fazer isso em cinco passos:
Passo 1: Cálculo da resistência de cada aparelho.
Usamos a fórmula da potência P = V² / R para encontrar a resistência de cada equipamento com base em seus valores nominais.
Resistência do Carregador (Rcarr):
Rcarr = V2nominal / Pnominal
Rcarr = (120 V)² / 90 W
Rcarr = 14400 / 90
Rcarr = 160 Ω
Resistência da Luminária (Rlum):
Rlum = V2nominal / Pnominal
Rlum = (120 V)² / 30 W
Rlum = 14400 / 30
Rlum = 480 Ω
Passo 2: Cálculo da resistência equivalente da associação em paralelo.
O carregador e a luminária estão em paralelo. A resistência equivalente de uma associação em paralelo ou Rp é dada por:
Substituindo os valores, temos:
Passo 3: Cálculo da resistência equivalente total do circuito.
O circuito total é composto pela resistência da régua (Rrégua) em série com a resistência equivalente do paralelo (Rp), ou:
Req = Rrégua + Rp
Req = 1 Ω + 120 Ω
Req = 121 Ω
Passo 4: Cálculo da corrente total do circuito.
Vamos usar a Primeira Lei de Ohm (V = R . i) com a tensão da tomada e a resistência equivalente total:
itotal = Vtomada / Req
itotal = 127 V / 121 Ω
itotal ≈ 1,05 A
Um erro comum seria usar os 120W de potência total para achar a corrente. Isso estaria incorreto, pois a tensão real sobre os aparelhos não será 127V nem 120V, devido à queda de tensão na resistência da régua.
Passo 5: Cálculo da potência dissipada na régua.
A corrente total (itotal) é a corrente que passa pela resistência da régua. Agora podemos calcular a potência dissipada nessa passagem:
Prégua = Rrégua . (itotal)²
Prégua = 1 . (127 / 121)²
Prégua ≈ 1 . (1,0495)²
Prégua ≈ 1,10 W
Continue praticando com exercícios de Associação de Resistores (comentados) e exercícios sobre Lei de Ohm (com respostas explicadas).
SOUTO, Ana. Exercícios sobre circuitos mistos (com respostas explicadas). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/exercicios-sobre-circuitos-mistos-com-respostas-explicadas/. Acesso em:


