MMC - Mínimo Múltiplo Comum

Rosimar Gouveia

Professora de Matemática e Física

O mínimo múltiplo comum (MMC) corresponde ao menor número inteiro positivo, diferente de zero, que é múltiplo ao mesmo tempo de dois ou mais números.

Lembre-se que para encontrar os múltiplos de um número, basta multiplicar esse número pela sequência dos números naturais.

Note que o zero (0) é múltiplo de todos os números naturais e que os múltiplos de um número são infinitos.

Para saber se um número é múltiplo de um outro, devemos descobrir se um é divisível pelo outro.

Por exemplo, 25 é múltiplo de 5, pois ele é divisível por 5.

Obs: Além do MMC, temos o MDC que corresponde ao máximo divisor comum entre dois números inteiros.

Como Calcular o MMC?

O cálculo do MMC, pode ser feito, através da comparação da tabuada desses números. Por exemplo, vamos descobrir o MMC de 2 e 3. Para isso, vamos comparar a tabuada de 2 e 3:

Note que o menor múltiplo em comum é o número 6. Portanto, dizemos que o 6 é o mínimo múltiplo comum (MMC) de 2 e 3.

Essa forma de encontrar o MMC é bem direta, mas quando temos números maiores ou mais de dois números, não é muito prática.

Para essas situações, o melhor é usar o método da fatoração, ou seja, decompor os números em fatores primos. Acompanhe, no exemplo abaixo, como calcular o MMC entre 12 e 45 usando esse método:

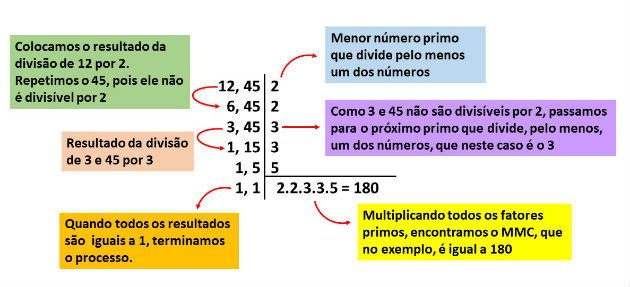
Observe que nesse processo vamos dividindo os elementos pelos números primos, ou seja, aqueles números naturais divisíveis por 1 e por ele mesmo: 2, 3, 5, 7, 11, 17, 19...

No final, multiplicam-se os números primos que foram utilizados na fatoração e encontramos o MMC.

Mínimo Múltiplo Comum e Frações

O mínimo múltiplo comum (MMC) é também muito utilizado em operações com frações. Sabemos que para somar ou subtrair frações é necessário que os denominadores sejam iguais.

Assim, calculamos o MMC entre os denominadores, e este passará a ser o novo denominador das frações.

Vejamos abaixo um exemplo:

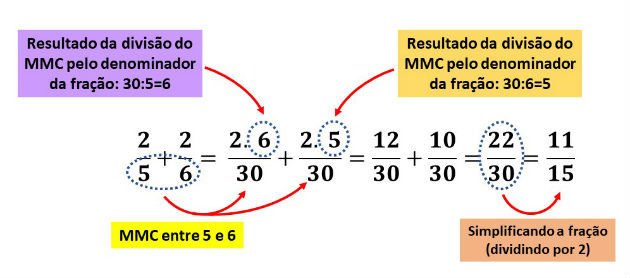
Como os denominadores são diferentes, o primeiro passo é encontrar o MMC entre 5 e 6. Fatorando, temos:

Agora que já sabemos que o MMC entre 5 e 6 é 30, podemos efetuar a soma, fazendo as seguintes operações, conforme indicado no diagrama abaixo:

Propriedades do MMC

• Entre dois números primos, o MMC será o produto entre eles.
• Entre dois números em que o maior é divisível pelo menor, o MMC será o maior deles.
• Ao multiplicar ou dividir dois números por um outro diferente de zero, o MMC aparece multiplicado ou dividido por esse outro.
• Ao dividir o MMC de dois números pelo máximo divisor comum (MDC) entre eles, o resultado obtido é igual ao produto de dois números primos entre si.
• Ao multiplicar o MMC de dois números pelo máximo divisor comum (MDC) entre eles, o resultado obtido é o produto desses números.

Leia também:

• Múltiplos
• Divisão
• Frações
• Adição e Subtração de Frações
• Múltiplos e Divisores

Exercícios de Vestibular com Gabarito

a) 54
b) 56
c) 58
d) 60
e) 62

2. (Vunesp) Para dividir os números 36 e 54 por respectivos menores números inteiros consecutivos de modo que se obtenham os mesmos quocientes em divisões exatas, esses números só podem ser, respectivamente:

a) 6 e 7
b) 5 e 6
c) 4 e 5
d) 3 e 4
e) 2 e 3

3. (Fuvest/SP) No alto da torre de uma emissora de televisão, duas luzes “piscam” com frequências diferentes. A primeira “pisca” 15 vezes por minuto e a segunda “pisca” 10 vezes por minuto. Se num certo instante, as luzes piscam simultaneamente, após quantos segundos elas voltarão a “piscar simultaneamente”?

a) 12
b) 10
c) 20
d) 15
e) 30

Saiba mais sobre MMC e MDCe teste seus conhecimentos em MMC e MDC - Exercícios.

Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.