Adição e Subtração de Frações
As frações representam as partes de um todo. A partir delas podem ser feitas operações de adição, subtração, multiplicação e divisão.
A Adição e Subtração de Frações é feita somando-se ou subtraindo-se os numeradores, conforme a operação. Quanto aos denominadores, desde que sejam iguais, mantêm a mesma base.
Lembre-se que nas frações, o termo superior é o numerador e o termo inferior é o denominador.
Exemplos:
E quando os denominadores são diferentes?
Quando os denominadores são diferentes é preciso igualá-los. Isto é feito a partir do mínimo múltiplo comum (MMC), que nada mais é do que o menor número capaz de dividir outro número.
Exemplo 1:
O MMC é 280, por quê?
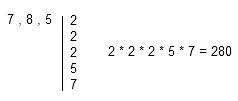
Após encontrar o MMC de 7, 8 e 5, temos de o dividir pelo denominador de cada fração e multiplicar pelo numerador. Assim:
280 /7 = 40 e 40 x 32 = 1280.
Por sua vez, 280 /8 = 35 e 35 x 19 = 665,
bem como 280/5 = 56 e 56 x 23 = 1288.
Exemplo 2:
O MMC é 18, por quê?
Após encontrar o MMC de 9 e 2, temos de o dividir pelo denominador de cada fração e multiplicar pelo numerador. Assim: 18/9 = 2 e 2 x 25 = 50.
Por sua vez, 18/2 = 9 e 9 x 20 = 180,
bem como 18/2 =9 e 9 x 42 = 378
Neste último exemplo, simplificamos a fração, o que significa que a reduzimos pelo seu divisor comum. Assim, tornamos a fração mais simples dividindo o numerador e o denominador pelo mesmo número: 248/2 = 124 e 18/2 = 9.
Exercícios comentados sobre adição e subtração de frações
Questão 1
Realize as operações com as frações a seguir e simplifique o resultado quando necessário.
a) 
.
com 
nos dá o resultado de b) 
.
(temos a subtração de frações com denominadores diferentes).
por 
nos dá o resultado c) 
.
(temos soma e subtração de frações com denominadores iguais).
com 
temos a fração 
e subtraindo Questão 2
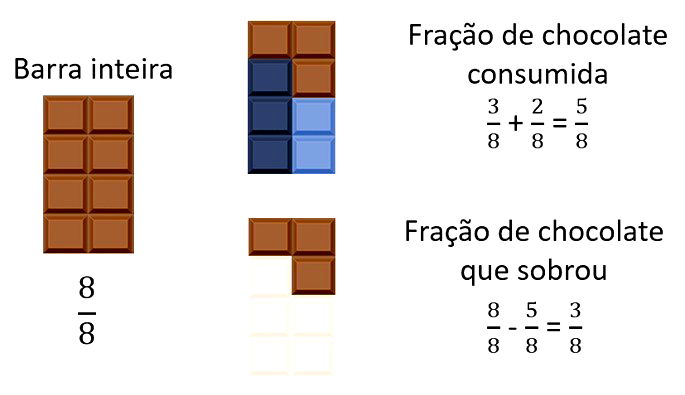
Comprei uma barra de chocolate que possuía um total de oito quadradinhos. Comi três quadradinhos de chocolate ontem e dois quadradinhos de chocolate hoje. Que fração de chocolate eu já comi? E que fração ainda falta comer?
a) Comi 5/8 e sobrou 3/8.
b) Comi 6/8 e sobrou 2/8.
c) Comi 3/8 e sobrou 5/8.
.
.
Questão 3
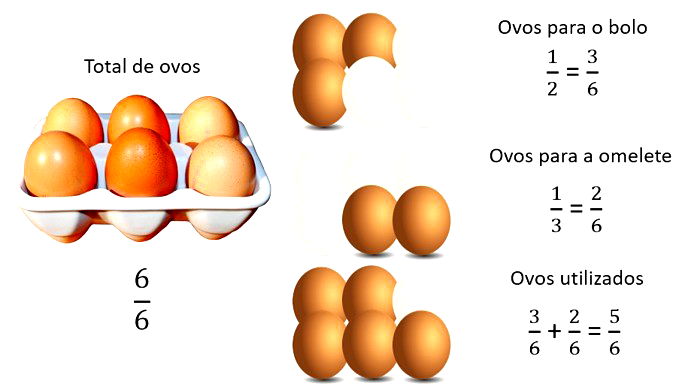
Ana tem uma caixa com 6 ovos. Ela pretende utilizá-los para fazer duas receitas. Para um bolo, é necessário utilizar a metade dos ovos e para fazer uma omelete é necessário utilizar um terço dos ovos. Quantos ovos Ana utilizou para fazer as duas receitas?
a) 4 ovos
b) 5 ovos
c) 6 ovos
de ovos para o bolo e 
de ovos para a omelete.
.
Pratique mais exercícios com:
- Exercícios sobre adição e subtração de frações
- Exercícios de Frações
- Exercícios sobre divisão e multiplicação de frações
Complemente seus estudos sobre o tema lendo os textos a seguir:
- Divisão de Fração
- O que é fração?
- Tipos de frações e operações fracionárias
- Multiplicação e Divisão de Frações
- Frações Equivalentes
- Fração Geratriz
Se busca um texto com abordagem para educação infantil, leia:
Adição e Subtração de Frações. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/adicao-e-subtracao-de-fracoes/. Acesso em:
