O que é fração?

Rafael C. Asth

Professor de Matemática e Física

Fração é a representação matemática das partes de determinada quantidade que foi dividida em pedaços ou fragmentos iguais.

As frações são úteis em várias situações, principalmente para representar algo que não conseguimos apresentar através de números naturais.

Escrita de uma fração e significado de cada termo

Vamos utilizar como exemplo a seguinte situação:

Maria comprou uma pizza e dividiu em 4 fatias iguais. Como não estava com muita fome, ela comeu apenas uma fatia. Que fração da pizza Maria conheceu?

Vemos no texto acima que das 4 fatias de pizza que Maria tinha, ela comeu apenas uma, ou seja, 1 de 4. Isso pode ser escrito como uma fração:

$tabela linha com célula com espaço 1 espaço em moldura inferior fecha moldura fim da célula seta para a esquerda numerador linha com 4 seta para a esquerda denominador linha com blank blank blank fim da tabela$

Os termos de uma fração são:

Numerador: vem do latim numeratus e significa “contar”.

Denominador: sua origem é do latim denominatus e significa “dar nome”.

No nosso exemplo, o número 1 representa o numerador da fração e indica quantas partes foram tomadas. Já o número 4, representa o denominador da fração e indica em quantas partes o todo foi dividida.

Por ter dividido a pizza em 4 partes iguais, então uma pizza inteira corresponde à fração $4 sobre 4$ .

$4 sobre 4 espaço igual a espaço 1$ , ou seja, um inteiro.

Regras para leitura das frações

O denominador de uma fração deve ser diferente de zero e é ele que dá nome a fração. Portanto, repetimos o numerador e mudamos a forma de pronunciar o denominador.

Quando o denominador está entre os números 2 e 9, lemos da seguinte forma: 2 (meio), 3 (terço), 4 (quarto), 5 (quinto), 6 (sexto), 7 (sétimo), 8 (oitavo) e 9 (nono).

Já as frações decimais, ou seja, com denominador 10, 100, 1000…, utilizamos a nomenclatura: 10 (décimos), 100 (centésimos), 1000 (milésimos), e assim por diante.

Para os demais números, ou seja, os que estão após o 9 e não são decimais, utilizamos a palavra avos após o denominador.

Veja a seguir exemplos de frações, seus termos e como devem ser lidas.

Fração	Numerador	Denominador	Leitura
$1 meio$	um	dois	um meio
$2 sobre 3$	dois	três	dois terços
$3 sobre 4$	três	quatro	três quartos
$7 sobre 8$	sete	oito	sete oitavos
$8 sobre 11$	oito	onze	oito onze avos
$7 sobre 21$	sete	vinte e um	sete vinte um avos
$9 sobre 10$	nove	dez	nove décimos
$9 sobre 100$	nove	cem	nove centésimos

Veja também: Tipos de frações e operações fracionárias

Tipos de frações

Fração mista

É formada por dois termos: um representa uma quantidade inteira e o outro corresponde à parte fracionária.

Exemplo:

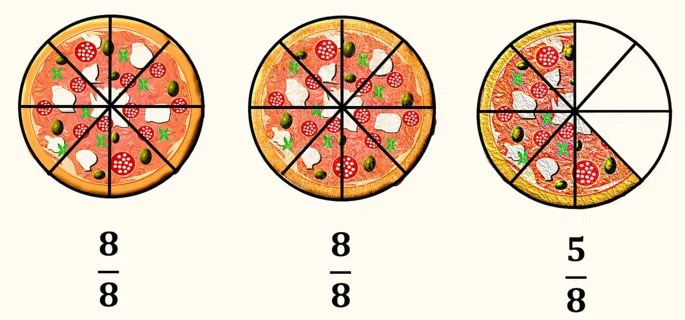
Observe que cada pizza foi dividida em 8 partes iguais e cada uma delas representa um inteiro, ou seja, $8 sobre 8$ .

A quantidade de pizza que vemos na imagem corresponde a duas pizzas inteiras, com 16 fatias, mais 5/8, ou seja, 5 fatias de uma pizza dividida em 8 partes.

Portanto, temos:

$numerador 21 espaço sobre denominador 8 fim da fração igual a numerador 8 espaço sobre denominador 8 fim da fração espaço mais espaço numerador 8 espaço sobre denominador 8 fim da fração espaço mais espaço 5 sobre 8 espaço igual a espaço 1 espaço mais espaço 1 espaço espaço mais 5 sobre 8 espaço igual a espaço 2 espaço mais espaço 5 sobre 8 espaço ou vírgula espaço simplesmente vírgula espaço 2 espaço 5 sobre 8.$

Lê-se a fração mista da seguinte forma: dois inteiros e cinco oitavos.

$tabela linha com blank célula com espaço espaço espaço 2 fim da célula célula com espaço espaço 5 espaço espaço em moldura inferior fecha moldura fim da célula blank blank blank linha com célula com parte espaço inteira fim da célula seta para baixo com canto para a esquerda 8 blank blank blank linha com blank blank seta para baixo blank blank blank linha com blank blank parte fracionária blank blank linha com blank blank blank blank blank blank fim da tabela$

Saiba mais sobre adição e subtração de frações.

Fração equivalente

Frações equivalentes são frações aparentemente diferentes, mas que representam a mesma parte do todo.

Exemplo: veja abaixo a quantidade de pizza consumida.

Ao dividir uma pizza em 8, 4 e 2 partes iguais, respectivamente, e comermos a metade dela, estaremos consumindo a mesma quantidade de pizza.

$4 sobre 8 igual a 2 sobre 4 igual a 1 meio$

Sendo assim, as frações $4 sobre 8$ , $2 sobre 4$ e $1 meio$ são frações equivalentes e representam a mesma quantidade.

Observe que a forma simplificada das frações $4 sobre 8$ e $2 sobre 4$ é $1 meio$ .

$4 à potência de dividido por 4 fim do exponencial sobre 8 à potência de dividido por 4 fim do exponencial igual a espaço numerador 1 espaço sobre denominador 2 fim da fração 2 à potência de dividido por 2 fim do exponencial sobre 4 à potência de dividido por 2 fim do exponencial igual a espaço numerador 1 espaço sobre denominador 2 fim da fração$

Ao simplificarmos as frações, dividindo o numerador e o denominador pelo mesmo número, chegamos a uma fração irredutível, que corresponde a uma fração que não mais pode ser simplificada.

Além dos exemplos vistos, as frações também são classificadas como:

Fração própria: fração menor que um inteiro, pois o numerador é menor que o denominador. Exemplo: $3 sobre 4$
Fração imprópria: fração maior que um inteiro, pois o numerador é maior que o denominador. Exemplo: $12 sobre 5$
Fração aparente: pode ser escrita como um número inteiro, pois o denominador é divisor do numerador. Exemplo: $4 sobre 2 igual a 2$
Fração geratriz: a divisão do numerador pelo denominador resulta em uma dízima periódica. Exemplo: $3 sobre 9 igual a 0 vírgula 333...$

Exercícios resolvidos sobre frações

Questão 1

Observe o quebra-cabeça abaixo e responda:

a) Que fração representa a parte não montada?

Ver Resposta

Resposta correta: 1/3 (Lê-se um terço).

Para escrever a fração primeiro é necessário descobrir o denominador, que corresponde ao total de peças necessários para preencher o quebra-cabeça.

Contando as peças, incluindo as que estão faltando, chegamos ao resultado de 9 peças. O numerador então será as peças que faltam, ou seja, 3.

A fração encontrada é $3 sobre 9$ . Entretanto, esse resultado ainda pode ser simplificado, pois 3 e 9 possuem um divisor em comum, que é o número 3.

$3 à potência de dividido por 3 fim do exponencial sobre 9 à potência de dividido por 3 fim do exponencial igual a 1 terço$

Simplificando os termos da fração, chegamos a fração que representa a parte não montada, que é $1 terço$ .

Aprenda mais sobre a simplificação de frações.

b) Que fração representa a parte montada?

Ver Resposta

Resposta correta: 2/3 (Lê-se dois terços).

Como vimos na alternativa anterior, o denominador da fração é 9, pois corresponde ao número total de peças do quebra-cabeça.

O numerador da fração pode ser calculado ao subtrairmos o número de peças totais pelo número de peças que faltam.

9 - 3 = 6

Sendo assim, colocando os valores na forma de fração, temos $6 sobre 9$ . Observe que esses números podem ser simplificados se dividirmos ambos por 3.

Após simplificarmos os termos da fração, descobrimos que a fração que representa a parte montada é $2 sobre 3$ .

Para mais questões, veja exercícios sobre frações.

c) Que fração representa o quebra-cabeça completo?

Ver Resposta

Resposta correta: 9/9

Essa fração pode ser encontrada somando a fração que corresponde à parte que falta e a fração correspondente à parte preenchida.

$3 sobre 9 espaço mais espaço 6 sobre 9 igual a 9 sobre 9$

As três peças que faltam mais as seis que já estão montadas nos dão o número 9 no numerador. Já o denominador corresponde ao total de peças, que é 9.

Observe que todas as peças do quebra-cabeça têm o mesmo tamanho. Isso é o que também acontece com uma fração, pois também representa a divisão em partes iguais.

Você também pode se interessar por multiplicação e divisão de frações.

Questão 2

Escreva na forma de fração mista e imprópria a fração que corresponde às fatias de pizza que contêm na imagem abaixo.

Ver Resposta

Resposta correta: fração mista 1 1/4 e fração imprópria 5/4.

O primeiro passo é atribuir a cada fatia de pizza a fração correspondente.

Veja que cada pizza foi dividida em 4 partes iguais. Portanto, cada fatia representa $1 quarto$ .

Somando as fatias de pizza que estão presentes na imagem, encontramos a fração imprópria, ou seja, o numerador é maior que o denominador.

$1 quarto espaço mais espaço 1 quarto espaço mais espaço 1 quarto espaço mais espaço 1 quarto espaço mais espaço 1 quarto espaço igual a espaço 5 sobre 4$

A fração mista consiste em separar a parte inteira da parte fracionária. Como temos uma pizza inteira e apenas 1 fatia na segunda pizza, a fração correspondente é:

$4 sobre 4 mais espaço 1 quarto igual a espaço 1 espaço mais 1 quarto espaço igual a espaço 1 espaço 1 quarto$

Portanto, a quantidade de pizza é 5/4, quando representada por uma fração imprópria, ou 1 1/4, na forma de fração mista.

Veja também

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.

Que tal um up?

Corretor de Redação
para o Enem Ferramenta Inteligente com feedback instantâneo

Exercícios exclusivos Acesso a centenas de questões com gabaritos

Estude sem publicidade Navegação limpa e focada para evitar distrações