Pêndulo simples: período, energia potencial e força restauradora

Rafael C. Asth

Professor de Matemática e Física

O pêndulo simples é um sistema composto por um fio inextensível, preso a um suporte, cuja extremidade contém um corpo de dimensões desprezíveis, que pode movimentar-se livremente.

Quando o instrumento está parado, ele permanece em uma posição fixa. Deslocar a massa presa na ponta do fio para determinada posição faz com que haja uma oscilação em torno do ponto de equilíbrio.

O movimento pendular ocorre com a mesma velocidade e aceleração à medida que o corpo passa pelas posições na trajetória que realiza.

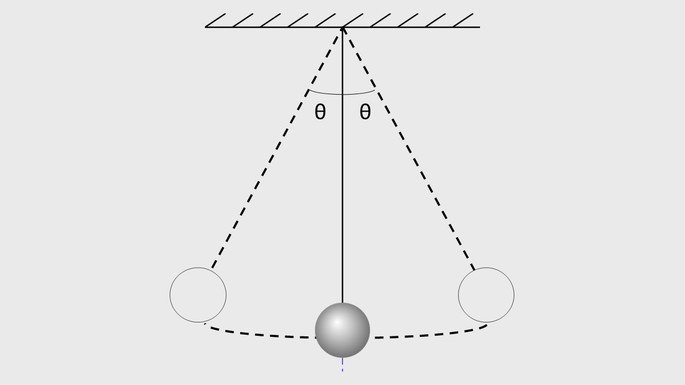
Em muitos experimentos o pêndulo simples é utilizado para determinar a aceleração da gravidade.

Galileu Galilei foi o primeiro a observar a periodicidade dos movimentos pendulares e propôs a teoria das oscilações do pêndulo.

Além do pêndulo simples existem outros tipos de pêndulos, como o pêndulo de Kater, que também mede a gravidade, e o pêndulo de Foucault, utilizado no estudo do movimento de rotação da Terra.

O pêndulo realiza um movimento harmônico simples, o MHS, e os principais cálculos realizados com o instrumento envolvem o período e a força restauradora.

Período do pêndulo (T)

O pêndulo simples realiza um movimento classificado como periódico, pois se repete nos mesmos intervalos de tempo e pode ser calculado através do período (T).

$começar estilo tamanho matemático 18px reto T espaço igual a 2 reto pi espaço raiz quadrada de reto L sobre reto g fim da raiz fim do estilo$

Onde,

T é o período, em segundos (s).
L é o comprimento do fio, em metros (m).
g é a aceleração da gravidade, em (m/s²).

Através do período, pode-se conhecer o menor intervalo de tempo para que o movimento ocorra e essa fórmula deve ser utilizada em pequenas oscilações, quando o ângulo é menor que 10º.

Veja também: Movimento Harmônico Simples

Força restauradora (F)

A força restauradora (F) é responsável por fazer com que o pêndulo retorne para sua posição de equilíbrio, já que a gravidade o direciona para o ponto mais baixo.

Pela posição para qual o corpo é direcionado no pêndulo, entende-se que a força restauradora é a componente horizontal da força peso. Por isso, sua fórmula é:

$começar estilo tamanho matemático 18px reto F com reto x subscrito espaço igual a espaço menos espaço reto K espaço. espaço reto x fim do estilo$

Onde,

F_x é a força restauradora, em newton (N).
x é o deslocamento da posição de equilíbrio, em metros (m).
K é a constante de proporcionalidade.

Conservação de energia no pêndulo

Observe a imagem abaixo. Um pêndulo simples está na sua posição de equilíbrio, representada pela letra A. Ao deslocá-lo para direita, é posicionado em B e ao soltá-lo alcança a posição C.

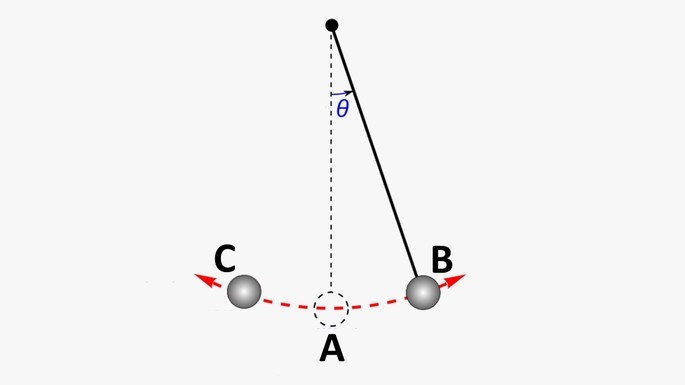
Na posição B, o corpo na extremidade do fio adquire energia potencial. Ao soltá-lo ocorre o movimento que vai até à posição C, fazendo com que adquira energia cinética, mas perca energia potencial ao diminuir a altura.

Quando o corpo sai da posição B e chega até a posição A, nesse ponto a energia potencial é nula, enquanto a energia cinética é máxima.

Desconsiderando a resistência do ar, pode-se admitir que o corpo nas posições B e C alcançam a mesma altura e, por isso, entende-se que o corpo possui a mesma energia do início.

Observa-se então que se trata de um sistema conservativo e a energia mecânica total do corpo permanece constante.

$reto E com reto M subscrito igual a espaço reto E com reto M com reto C subscrito subscrito fim do subscrito espaço mais espaço espaço reto E com reto M com reto P subscrito subscrito fim do subscrito espaço igual a espaço cte.$

Sendo assim, em qualquer ponto da trajetória a energia mecânica será a mesma.

$reto E com reto M com reto B subscrito subscrito fim do subscrito igual a espaço reto E com reto M com reto A subscrito subscrito fim do subscrito espaço igual a espaço espaço reto E com reto M com reto C subscrito subscrito fim do subscrito espaço igual a espaço cte.$

Veja também:

Exercícios resolvidos sobre pêndulo simples

Exercício 1

Se o período de um pêndulo é de 2s, qual o comprimento do seu fio inextensível se no local onde o instrumento encontra-se a aceleração da gravidade é de 9,8 m/s²?

Ver Resposta

Resposta correta: 1 m.

Para descobrir o comprimento do pêndulo, primeiro é necessário substituir os dados do enunciado na fórmula do período.

$reto T espaço igual a 2 reto pi espaço raiz quadrada de reto L sobre reto g fim da raiz 2 espaço s espaço igual a espaço espaço raiz quadrada de numerador reto L sobre denominador 9 vírgula 8 fim da fração fim da raiz numerador 2 espaço s sobre denominador 2 reto pi fim da fração igual a espaço espaço raiz quadrada de numerador reto L sobre denominador 9 vírgula 8 espaço reto m dividido por reto s ao quadrado fim da fração fim da raiz 0 vírgula 32 espaço reto s espaço igual a espaço raiz quadrada de numerador reto L sobre denominador 9 vírgula 8 espaço reto m dividido por reto s ao quadrado fim da fração fim da raiz$

Para remover a raiz quadrada da equação, precisamos elevar os dois termos ao quadrado.

$parêntese esquerdo 0 vírgula 32 espaço reto s parêntese direito ao quadrado espaço igual a espaço abre parênteses raiz quadrada de numerador reto L sobre denominador 9 vírgula 8 espaço reto m dividido por reto s ao quadrado fim da fração fim da raiz fecha parênteses ao quadrado espaço 0 vírgula 1024 espaço s ao quadrado espaço igual a espaço numerador reto L sobre denominador 9 vírgula 8 espaço reto m dividido por reto s ao quadrado fim da fração 0 vírgula 1024 espaço riscado diagonal para cima sobre reto s ao quadrado fim do riscado espaço reto x espaço 9 vírgula 8 espaço reto m dividido por riscado diagonal para cima sobre reto s ao quadrado fim do riscado igual a espaço reto L reto L espaço aproximadamente igual espaço 1 espaço reto m$

Sendo assim, o comprimento do pêndulo é de aproximadamente um metro.

Exercício 2

(UFRS) Um pêndulo simples, de comprimento L, tem um período de oscilação T, num determinado local. Para que o período de oscilação passe a valer 2T, no mesmo local, o comprimento do pêndulo deve ser aumentado em:

a) 1 L.
b) 2 L.
c) 3 L.
d) 5 L.
e) 7 L.

Ver Resposta

Alternativa correta: c) 3 L.

A fórmula para calcular o período de oscilação de um pêndulo é:

$reto T espaço igual a 2 reto pi espaço raiz quadrada de reto L sobre reto g fim da raiz$

Adotando L_icomo o comprimento inicial, essa grandeza é diretamente proporcional ao período T. Dobrando o período para 2T, o Lf deve ser quatro vezes o L_i, pois deve-se extrair a raiz desse valor.

L_f= 4L_i

Como a pergunta é quanto se deve aumentar, basta encontrar a diferença entre o valor inicial e final do comprimento.

L_f– L_i = 4L_i– Li = 3L_i

Logo, o comprimento deve ser três vezes maior que o inicial.

Exercício 3

(PUC-PR) Um pêndulo simples oscila, num local onde a aceleração da gravidade é 10 m/s², com um período de oscilação igual a $reto pi$ /2 segundos. O comprimento deste pêndulo é:

a) 1,6 m
b) 0,16 m
c) 62,5 m
d) 6,25 m
e) 0,625 m

Ver Resposta

Alternativa correta: e) 0,625 m.

Substituindo os valores na fórmula, temos:

$reto T espaço igual a 2 reto pi espaço raiz quadrada de reto L sobre reto g fim da raiz numerador reto pi espaço sobre denominador 2 fim da fração igual a 2 reto pi espaço raiz quadrada de reto L sobre 10 fim da raiz$

Para eliminar a raiz quadrada, elevamos os dois membros da equação ao quadrado.

$parêntese esquerdo reto pi sobre 2 parêntese direito ao quadrado espaço igual a parêntese esquerdo 2 reto pi espaço raiz quadrada de reto L sobre 10 fim da raiz parêntese direito ao quadrado espaço 1 quarto espaço igual a espaço 4. reto L sobre 10$

Agora, basta resolvê-la e encontrar o valor de L.

$reto L espaço igual a espaço numerador 1.10 sobre denominador 4.4 fim da fração reto L espaço igual a espaço 10 sobre 16 reto L espaço igual a 0 vírgula 625 espaço$

Veja também Equilíbrio estático e dinâmico.

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.