🔥 Poupe agora com 30% OFF no TM+ e estude melhor o ano inteiro

Poupe agora com 30% OFF no TM+ e estude melhor o ano inteiro

Área do Triângulo: aprenda como calcular (com exemplos e exercícios)

Revisão por Rafael C. Asth

Professor de Matemática e Física

A área do triângulo pode ser calculada através das medidas da base e da altura da figura. Lembre-se que o triângulo é uma figura geométrica plana formada por três lados.

Contudo, há diversas maneiras de calcular a área de um triângulo, sendo que a escolha é feita conforme os dados conhecidos no problema.

Acontece que muitas vezes, não temos todas as medidas necessárias para fazer esse cálculo.

Nestes casos, devemos identificar o tipo de triângulo (retângulo, equilátero, isósceles ou escaleno) e considerar as suas características e propriedades para encontrar as medidas que necessitamos.

Fórmulas para calcular a área de um triângulo

Na maioria das situações, usamos as medidas da base e da altura de um triângulo para calcular a sua área. Considere o triângulo representado abaixo, sua área será calculada, usando a seguinte fórmula:

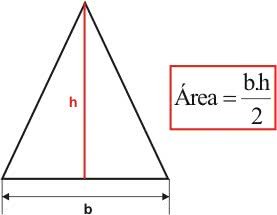
área do triângulo isósceles

Sendo,

Área: área do triângulo
b: base
h:altura

Exemplo:
Um triângulo de base igual a 6 m possui altura de 3 m. Determine a área deste triângulo.

Resolução:
Para determinar a área deste triângulo, substituímos seus valores na fórmula:

$reto A igual a numerador reto b espaço. espaço reto h sobre denominador 2 fim da fração reto A igual a numerador 6 espaço. espaço 3 sobre denominador 2 fim da fração reto A igual a 18 sobre 2 reto A igual a 9 espaço reto m ao quadrado$

Note que a unidade de área deve estar elevada ao quadrado.

Área do Triângulo Retângulo

O triângulo retângulo possui um ângulo reto (90º), e dois ângulos agudos (menores que 90º). Desta maneira, das três alturas de um triângulo retângulo, duas coincidem com os lados desse triângulo.

Além disso, se conhecermos dois lados de um triângulo retângulo, usando o teorema de Pitágoras, encontramos facilmente o terceiro lado.

Assim, calculamos a área de um triângulo retângulo como o caso geral anterior. No triângulo retângulo, a altura e a base são seus catetos.

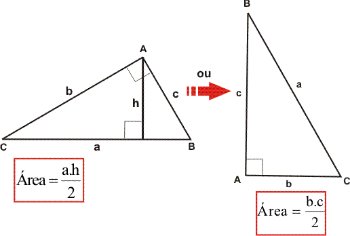
Exemplo:
Um triângulo retângulo possui os catetos iguais a 3 e 4 metros. Determine sua área.

Resolução:
Como na situação anterior, utilizaremos a fórmula básica, desta vez com o 3 e o 4 como altura e base.

$reto A igual a numerador reto b espaço. espaço reto h sobre denominador 2 fim da fração reto A igual a numerador 4 espaço. espaço 3 sobre denominador 2 fim da fração reto A igual a 12 sobre 2 reto A espaço igual a espaço 6 espaço reto m ao quadrado$

A ordem na multiplicação entre o 3 o 4 não altera o resultado.

Área do Triângulo Equilátero

O triângulo equilátero, também chamado de equiângulo, é um tipo de triângulo que possui todos os lados e ângulos internos congruentes (mesma medida).

Neste tipo de triângulo, quando conhecemos apenas a medida do lado, podemos usar o teorema de Pitágoras para encontrar a medida da altura.

A altura, neste caso, o divide em outros dois triângulos congruentes. Considerando um desses triângulos e que seus lados são L, h (altura) e L/2 (o lado relativo a altura fica dividido ao meio), ficamos com:

$L ao quadrado igual a h ao quadrado mais abre parênteses L sobre 2 fecha parênteses ao quadrado seta dupla para a direita h ao quadrado igual a L ao quadrado menos L sobre 4 ao quadrado seta dupla para a direita h igual a índice radical espaço em branco de numerador 3 L ao quadrado sobre denominador 4 fim da fração fim da raiz seta dupla para a direita h igual a numerador raiz quadrada de 3 espaço L sobre denominador 2 fim da fração$

Assim, substituindo o valor encontrado para a altura na fórmula da área, temos:

Remover anúncios

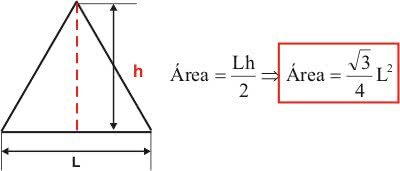
Exemplo:
Um triângulo possui seus lados com medidas iguais a 12 m. Determine sua área.

Resolução:
Como os lados possuem mesma medida, é um triângulo equilátero. Ao invés de calcular a altura, podemos utilizar uma fórmula mais apropriada, simplificando o trabalho.

$reto A igual a numerador raiz quadrada de 3 sobre denominador 4 fim da fração reto L ao quadrado reto A igual a numerador raiz quadrada de 3 sobre denominador 4 fim da fração espaço. espaço 12 ao quadrado reto A igual a numerador raiz quadrada de 3 sobre denominador 4 fim da fração espaço. espaço 144 reto A igual a 36 raiz quadrada de 3 espaço reto m ao quadrado$

Área do Triângulo Isósceles

O triângulo isósceles é um tipo de triângulo que possui dois lados e dois ângulos internos congruentes. Para calcular a área do triângulo isósceles, utiliza-se a fórmula básica para um triângulo qualquer.

Quando queremos calcular a área de um triângulo isósceles e não conhecemos a medida da altura, também podemos usar o teorema de Pitágoras para encontrar essa medida.

No triângulo isósceles, a altura relativa à base (lado com medida diferente dos outros dois lados) divide este lado em dois segmentos congruentes (mesma medida).

Desta forma, conhecendo as medidas dos lados de um triângulo isósceles, podemos encontrar sua área.

Exemplo: Calcule a área do triângulo isósceles representado na figura abaixo:

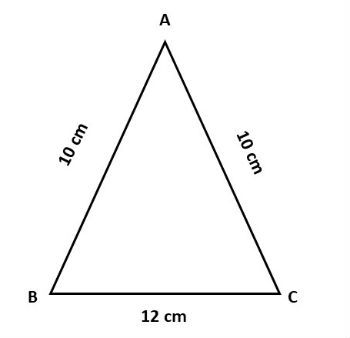
Resolução:

Para calcular a área do triângulo usando a fórmula básica, precisamos conhecer a medida da altura. Considerando a base como o lado de diferente medida, iremos calcular a altura relativa a esse lado.

Passo 1: Determinar a altura.

A altura forma um triângulo retângulo com base 6 cm e hipotenusa 10 cm.

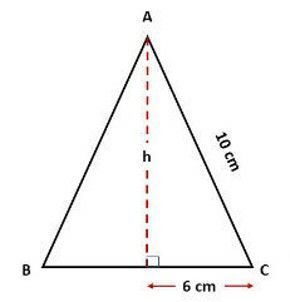
Pelo Teorema de Pitágoras:

$10 ao quadrado igual a reto h ao quadrado mais 6 à potência de 6 100 igual a reto h ao quadrado mais 36 64 igual a reto h ao quadrado raiz quadrada de 64 igual a reto h 8 espaço igual a espaço reto h$

A altura tem 8 cm.

Passo 2: determinar a área do triângulo original.

Utilizamos a fórmula básica para determinar a área do triângulo original.

$reto A igual a numerador reto b espaço. espaço reto h sobre denominador 2 fim da fração reto A igual a numerador 12 espaço. espaço 8 sobre denominador 2 fim da fração reto A igual a 96 sobre 2 reto A igual a 48 espaço cm ao quadrado$

Área do Triângulo Escaleno

O triângulo escaleno é um tipo de triângulo que possui todos os lados e ângulos internos diferentes. Sendo assim, uma forma de encontrar a área desse tipo de triângulo é usar a trigonometria.

Se conhecermos dois lados desse triângulo e o ângulo entre esses dois lados, sua área será dada por:

Remover anúncios

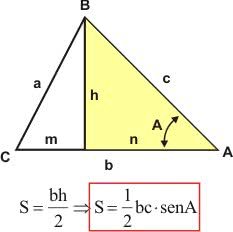
Pela Fórmula de Heron também podemos calcular a área do triângulo escaleno.

Exemplo:
Um triângulo escaleno possui dois lados conhecidos com medidas de 12 m e 9 m. Estes lados formam um ângulo de 30º entre si. Determine a área deste triângulo.

Resolução:
Não conhecemos a altura, mas os dados nos permitem utilizar a seguinte fórmula:

$A igual a numerador 12 espaço. espaço 9 espaço. espaço s e n espaço 30 º sobre denominador 2 fim da fração$

Da trigonometria, sabemos que o seno de um ângulo de 30º é igual a 0,5.

$reto A igual a numerador 12 espaço. espaço 9 espaço. espaço 0 vírgula 5 sobre denominador 2 fim da fração reto A igual a 54 sobre 2 reto A igual a 27 espaço reto m ao quadrado$

Outras fórmulas para calcular a área do triângulo

Além de encontrar a área através do produto da base pela altura e dividir por 2, podemos também utilizar outros processos.

Fórmula de Heron

Outra maneira de calcular a área do triângulo é pela "Fórmula de Heron", também chamada de "Teorema de Herão". Ela utiliza os semiperímetros (metade do perímetro) e os lados do triângulo.

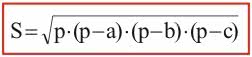
Onde,

S: área do triângulo
p: semiperímetro
a, b e c: lados do triângulo

Sendo o perímetro do triângulo a soma de todos os lados da figura, o semiperímetro representa a metade do perímetro:

$p igual a numerador a mais b mais c sobre denominador 2 fim da fração$

Exemplo:
Um triângulo possui os lados medindo 10 m, 17 m e 21 m. Calcule sua área.

Resolução:
Cálculo do Semiperímetro:

$p igual a numerador 10 espaço mais espaço 17 espaço mais espaço 21 sobre denominador 2 fim da fração p igual a 48 sobre 2 p igual a 24$

Substituindo na Fórmula de Heron:

$reto S igual a raiz quadrada de reto p espaço. espaço parêntese esquerdo reto p menos reto a parêntese direito espaço. espaço parêntese esquerdo reto p menos reto b parêntese direito espaço. espaço parêntese esquerdo reto p menos reto c parêntese direito fim da raiz reto S igual a raiz quadrada de 24 espaço. espaço parêntese esquerdo 24 menos 10 parêntese direito espaço. espaço parêntese esquerdo 24 menos 17 parêntese direito espaço. espaço parêntese esquerdo 24 menos 21 parêntese direito fim da raiz reto S igual a raiz quadrada de 24 espaço. espaço parêntese esquerdo 14 parêntese direito espaço. espaço parêntese esquerdo 7 parêntese direito espaço. espaço parêntese esquerdo 3 parêntese direito fim da raiz reto S igual a raiz quadrada de 7056 reto S igual a 84 espaço reto m ao quadrado$

Interessante notar que, nesta fórmula não há a necessidade de se conhecer a medida da altura (h), por isso, quando essa informação não é dada, o "Teorema de Heron" facilita encontrar a área do triângulo.

Remover anúncios

Fórmula do Raio Circunscrito

Baseada na "Lei dos Senos" tem-se a "Fórmula do Raio Circunscrito" representada pela expressão:

Neste caso, o triângulo está na circunferência. Seus três vértices estão sobre a linha da circunferência.

$A igual a numerador a. b. c sobre denominador 4. r fim da fração$

A: área do triângulo
a, b e c: lados do triângulo
r: raio da circunferência circunscrita

Exemplo:
Um triângulo com lados 5, 12 e 13 cm está inscrito em uma circunferência. Sabendo que o raio da circunferência é de 6,5 cm, qual é a área ocupada pelo triângulo?

Resolução:
$A igual a numerador a. b. c sobre denominador 4. r fim da fração A igual a numerador 5.12.13 sobre denominador 4.6 vírgula 5 fim da fração A igual a 780 sobre 26 A igual a 30 espaço c m ao quadrado$

Questões de vestibular (com gabarito)

Questão 1

(Enem - 2010) Em canteiros de obras de construção civil, é comum perceber trabalhadores realizando medidas de comprimento e de ângulos e fazendo demarcações por onde a obra deve começar ou se erguer.

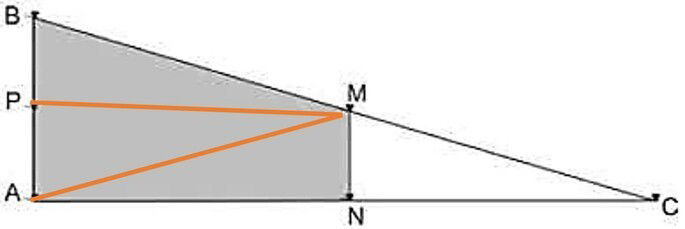
Em um desses canteiros foram feitas algumas marcas no chão plano. Foi possível perceber que, das seis estacas colocadas, três eram vértices de um triângulo retângulo e as outras três eram os pontos médios dos lados desse triângulo conforme pode ser visto na figura, em que as estacas foram indicadas por letras.

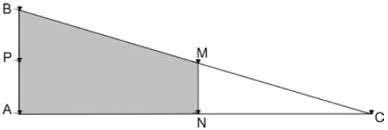
A região demarcada pelas estacas A, B, M e N deveria ser calçada com concreto. Nessas condições, a área a ser calçada corresponde

a) à mesma área do triângulo AMC.
b) à mesma área do triângulo BNC.
c) à metade da área formada pelo triângulo ABC.
d) ao dobro da área do triângulo MNC.
e) ao triplo da área do triângulo MNC.

Ver Resposta

Alternativa e: ao triplo da área do triângulo MNC.

Podemos dividir o triângulo ABC em quatro triângulos iguais.

O triângulo AMN tem a mesma área do triângulo NMC, pois eles possuem a mesma altura (NM) e a mesma base, uma vez que N é o ponto médio de AC (AN = NC).

Como a fórmula básica da área do triângulo diz que a área é base vezes altura dividido por 2, esses triângulos têm a mesma área.

Esse mesmo raciocínio é usado para provar que APM e PBM possuem áreas iguais ao triângulo NMC.

Assim, para responder a questão, verificamos que a parte pintada possui três triângulos, ou seja, é três vezes maior que NMC.

Questão 2

(Cefet/RJ - 2014) Se ABC é um triângulo tal que AB = 3 cm e BC = 4 cm, podemos afirmar que a sua área, em cm², é um número:

Remover anúncios

a) no máximo igual a 9
b) no máximo igual a 8
c) no máximo igual a 7
d) no máximo igual a 6

Ver Resposta

Alternativa d: no máximo igual a 6

Para dois lados fixos de um triângulo, a área é máxima quando esses lados formam um ângulo de 90° (são perpendiculares).

$A igual a numerador 3 espaço. espaço 4 sobre denominador 2 fim da fração A igual a 6 espaço c m ao quadrado$

Questão 3

(PUC/RIO - 2007) A hipotenusa de um triângulo retângulo mede 10 cm e o perímetro mede 22 cm. A área do triângulo (em cm²) é:

a) 50
b) 4
c) 11
d) 15
e) 7

Ver Resposta

Alternativa c: 11

Vamos nomear os lados do triângulo:

a será hipotenusa;
b e c serão catetos.

Pelo Teorema de Pitágoras:

$bold italic b à potência de negrito 2 negrito mais bold italic c à potência de negrito 2 negrito espaço negrito igual a bold italic a à potência de negrito 2$

Pela informação do perímetro:

$a espaço mais espaço b espaço mais espaço c espaço igual a 22 b espaço mais espaço c espaço igual a espaço 22 espaço menos espaço a b espaço mais espaço c espaço igual a espaço 22 espaço menos espaço 10 bold italic b negrito espaço negrito mais negrito espaço bold italic c negrito espaço negrito igual a negrito espaço negrito 12$

Com estas equações, formamos o sistema:

$abre chaves atributos de tabela alinhamento de coluna left fim dos atributos linha com célula com b ao quadrado mais c ao quadrado igual a 10 ao quadrado fim da célula linha com célula com b espaço mais espaço c espaço igual a espaço 12 fim da célula fim da tabela fecha$

Para resolver este sistema, vamos elevar ambos os membros da segunda equação ao quadrado.

$parêntese esquerdo b espaço mais espaço c parêntese direito ao quadrado igual a 12 ao quadrado b ao quadrado mais espaço 2 b c espaço mais espaço c ao quadrado igual a 144$

Organizando melhor a segunda linha:

$b ao quadrado mais espaço c ao quadrado espaço mais 2 b c espaço igual a 144$

Da equação 1 do sistema, $b ao quadrado mais c ao quadrado igual a 10 ao quadrado$ . Substituindo:

$b ao quadrado mais espaço c ao quadrado espaço mais 2 b c espaço igual a 144 10 ao quadrado espaço mais 2 b c espaço igual a 144 100 espaço mais 2 b c espaço igual a 144 2 b c igual a 144 menos 100 2 b c igual a 44 b c igual a 44 sobre 2 b c igual a 22$

Assim, a base b e a altura c multiplicados resultam em 22, mas a fórmula da área diz que ela é igual a:

$A igual a numerador b c sobre denominador 2 fim da fração$

Logo, para determinar a área, basta dividir por 2.

22 / 2 = 11

Continue os seus estudos:

Faça mais exercícios:

Revisão por Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.

Edição por Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.

Remover anúncios