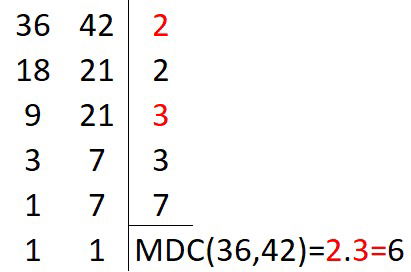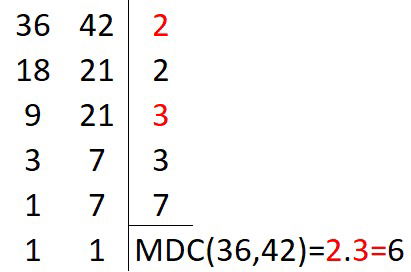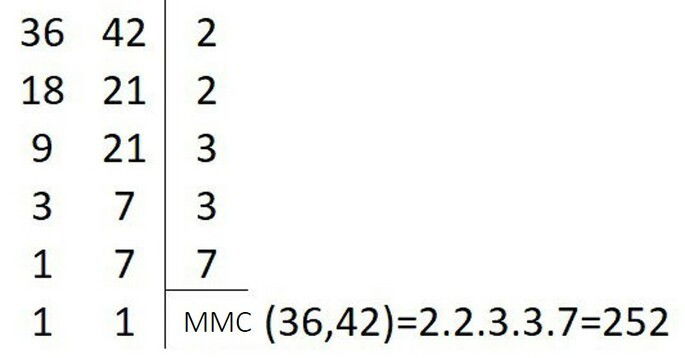Exercícios sobre Máximo Divisor Comum (MDC)

Rafael C. Asth

Professor de Matemática e Física

Estude com os exercícios sobre Máximo Divisor Comum (MDC) e tire suas dúvidas com as resoluções detalhadas passo a passo.

Questão 1

Calcule o MDC entre 180 e 150.

Ver Resposta

Para calcular o MDC entre 180 e 150, devemos realizar a decomposição em fatores primos e multiplicar os que dividem, simultaneamente, as duas colunas.

cálculo do MDC entre 180 e 150 cujo resultado é 30

Repare que os números em vermelho representam os divisores que devem ser multiplicados para determinação do MDC. Estes dividiram números nas duas colunas, simultaneamente.

Portanto, o Maior Divisor Comum entre 180 e 150 é o 30.

Questão 2

Joana está preparando kits de doces para distribuir entre alguns convidados. Há 36 brigadeiros e 42 cajuzinhos. Ela quer separá-los em pratos de modo a ocupar a menor quantidade de pratos mas, que todos os pratos tenham a mesma quantidade de doces e sem misturá-los. A quantidade de doces que Joana deverá colocar em cada prato, será

a) 21.
b) 12.
c) 6.
d) 8.
e) 5.

Ver Resposta

Resposta correta: c) 6.

Para encontrar a menor quantidade de pratos a serem utilizados, será necessário colocar a maior quantidade de doces em cada prato, mas fazendo com que todos os pratos tenham a mesma quantidade de doces e, sem misturar brigadeiros e cajuzinhos.

Para isso, é necessário encontrar o maior divisor comum entre 36 e 42. Fazendo a fatoração:

A quantidade de doces em cada prato será de 6 doces.

Questão 3

Um evento de corrida de equipes irá acontecer no próximo final de semana e, o período para as inscrições de participantes terminou hoje. Ao total, 88 pessoas se inscreveram, sendo 60 mulheres e 28 homens. Para as duas modalidades, feminina e masculina, as equipes devem possuir sempre, o mesmo e o maior número e atletas possível sem misturar homens e mulheres em uma mesma equipe. Desta forma o número de atletas em cada equipe será de

a) 10.
b) 8.
c) 6.
d) 4.
e) 2.

Ver Resposta

Resposta correta: d) 4.

Para saber o maior número de atletas possível em cada equipe, de modo que todas tenham o mesmo número de atletas, sem misturar homens e mulheres em uma mesma equipe, devemos dividir a quantidade de inscritos, homens e mulheres, pelo Maior Divisor Comum entre os dois.

Para determinar o MDC(28,60), fazemos a fatoração.

Questões de vestibulares e concursos

Questão 4

(Correios – Cespe). O piso de uma sala retangular, medindo 3,52 m × 4,16 m, será revestido com ladrilhos quadrados, de mesma dimensão, inteiros, de forma que não fique espaço vazio entre ladrilhos vizinhos. Os ladrilhos serão escolhidos de modo que tenham a maior dimensão possível.

Na situação apresentada, o lado do ladrilho deverá medir

a) mais de 30 cm.
b) menos de 15 cm.
c) mais de 15 cm e menos de 20 cm.
d) mais de 20 cm e menos de 25 cm.
e) mais de 25 cm e menos de 30 cm

Ver Resposta

Resposta correta: a) mais de 30 cm.

Note que os dados da questão estão em metros e as respostas em centímetros. Sendo assim, vamos passar os valores da questão para centímetros.

3,52 m = 352 cm
4,16 m = 416 cm

Como o piso é quadrado, todos os lados devem possuir a mesma medida. Por isso, a medida do lado deve ser um divisor comum para 352 e 416.

Vamos determinar o Maior Divisor Comum em 352 e 416.

Desta forma, a resposta é a letra a, o ladrilho deverá medir mais que 30 cm.

Questão 5

(Professor de Matemática da Educação Básica - 2019) Um ferreiro vai confeccionar pedaços de barras de ferro de mesma medida. Ele dispõe de 35 barras de 270 cm, 18 de 540 cm e 6 de 810 cm, todas de igual largura. Ele pretende cortar as barras em pedaços de mesmo comprimento, sem deixar sobras, de modo que esses pedaços fiquem o maior possível, mas de comprimento menor que 1 m. Quantas pedaços de barra de ferro o ferreiro pode produzir?

a) 89.
b) 178.
c) 267.
d) 524.
e) 801.

Ver Resposta

Resposta correta: c) 267.

O comprimento dos novos pedaços devem dividir de forma exata as barras já disponíveis, de modo que todas tenham o mesmo e o maior comprimento mas, menores que 1 m.

Para isso, devemos fatorar as medidas.

O MDC é 270 cm. No entanto, é preciso que os novos pedaços sejam menores que 100 cm.

Se retirarmos o fator 2, e multiplicarmos os que restaram em destaque na fatoração, teríamos:

3.3.3.5 = 135 cm, ainda maior que 100 cm.

Retirando um fator 3, e multiplicarmos os que restaram em destaque na fatoração, teríamos:

2.3.3.5 = 90 cm

Sendo assim, os novos pedaços devem possuir 90 cm. Para saber a quantidade, devemos dividir cada medida de barra já disponível por 90 e multiplicar pelas quantidades de cada.

$270 espaço c m espaço dividido por espaço 90 espaço c m espaço igual a espaço 3$
Como há 35 barras de 270, fazemos a multiplicação:
$35 sinal de multiplicação 3 igual a 105 espaço b a r r a s$

$540 espaço c m dividido por 90 espaço c m igual a 6$
Como há 18 barras de 540, fazemos a multiplicação:
$18 sinal de multiplicação 6 igual a 108 espaço b a r r a s$

$810 espaço c m espaço dividido por espaço 90 espaço c m igual a 9$
Como há 18 barras de 540, fazemos a multiplicação:
$6 sinal de multiplicação 9 igual a 54 espaço b a r r a s$

Somando as quantidades individuais 105 + 108 + 54 = 267.

Portanto, ferro o ferreiro pode produzir 267 pedaços de barra de ferro.

Questão 6

(Prefeitura de Areial Professor B - Matemática 2021) O gerente de uma loja de aparelhos eletrônicos, apaixonado por matemática, propõe que o preço de um determinado celular seja dado em reais pela expressão mdc (36,42). mmc (36,42).
Neste caso, é CORRETO afirmar que o valor do celular, em reais, é igual a:

a) R$ 1,812,00
b) R$ 1,612,00
b) R$ 1,712,00
d) R$ 2,112,00
e) R$ 1,512,00

Ver Resposta

Resposta correta: e) R$ 1,512,00.

Primeiro vamos calcular o MDC(36,42).

Para isso, basta fatorar os números e multiplicar os fatores que dividem, simultaneamente, as duas colunas.

Para o cálculo do MMC, basta multiplicarmos todos os fatores.

Agora, basta multiplicar os dois resultados.

252 . 6 = 1512

O valor do celular, em reais, é igual a R$ 1512,00.

Questão 7

(Prefeitura de Irati - SC - Professor de Inglês) Em uma caixa, há 18 bolinhas azuis, 24 bolinhas verdes e 42 bolinhas vermelhas. Marta quer organizar as bolinhas em sacolas, de modo que cada sacola tenha o mesmo número de bolinhas e cada cor fique igualmente distribuídas nas sacolas e que possa usar a quantidade máxima de sacolas possíveis para isso. Qual a soma das bolinhas azuis, verdes e vermelhas que ficaram em cada sacola?

a) 7
b) 14
c) 12
d) 6

Ver Resposta

Resposta correta: b) 14.

Primeiramente, vamos determinar o maior divisor comum aos três números;

Agora, basta dividir a quantidade de bolinhas de cada cor por 6 e, somar o resultado.

$18 dividido por 6 igual a 3 24 dividido por 6 igual a 4 42 dividido por 6 igual a 7 S o m a n d o espaço o s espaço r e s u l t a d o s 3 mais 4 mais 7 igual a 14$

Questão 8

(USP-2019) A função E de Euler determina, para cada número natural ݊n, a quantidade de números naturais menores do que ݊n cujo máximo divisor comum com ݊n é igual a 1. Por exemplo, E (6) = 2 pois os números menores do que 6 com tal propriedade são 1 e 5. Qual o valor máximo de E (n), para ݊n de 20 a 25?

a) 19
b) 20
c) 22
d) 24
e) 25

Ver Resposta

Resposta correta: c) 22.

E (n) é uma função que fornece o número de vezes em que o MDC entre o número n, e um número natural menor que n, é igual a 1.

Devemos determinar para n entre 20 e 25, qual deles retorna E (n) maior.

Lembre-se que os números primos só são divisíveis por 1 e por eles próprios. Por isso, são os que apresentarão E (n) maiores.

Entre 20 e 25, apenas o 23 é número primo. Como E (n) compara o MDC entre n e um número menor que n, temos que E (23) = 22.

Portanto, o valor máximo de E (n), para ݊n de 20 a 25, ocorre para n=23, sendo: E(23) = 22.

Apenas para melhorar a compreensão:

MDC(1,23)=1
MDC(2,23)=1
.
.
.
MDC(22,23)=1

Questão 9

(PUC-PR Medicina 2015) Um estagiário recebeu a tarefa de organizar documentos em três arquivos. No primeiro arquivo, havia apenas 42 contratos de locação; no segundo arquivo, apenas 30 contratos de compra e venda; no terceiro arquivo, apenas 18 laudos de avaliação de imóveis. Ele foi orientado a colocar os documentos em pastas, de modo que todas as pastas devem conter a mesma quantidade de documentos. Além de não poder mudar algum documento do seu arquivo original, deveria colocar na menor quantidade possível de pastas. O número mínimo de pastas que ele pode usar é:

a) 13.
b) 15.
c) 26.
d) 28.
e) 30.

Ver Resposta

Resposta correta: b) 15.

Calculamos o MDC(18,30,42)

Agora, dividimos as quantidades de documentos em cada arquivo por 6 e, somamos o resultado.

$18 dividido por 6 igual a 3 30 dividido por 6 igual a 5 42 dividido por 6 igual a 7$

$S o m a n d o espaço o s espaço r e s u l t a d o s 3 mais 5 mais 7 igual a 15$

Desse modo, 15 é o número mínimo de pastas que ele pode usar.

Exercite mais com MMC e MDC - Exercícios.

Você também pode aprender mais com:

MDC - Máximo Divisor Comum
MMC e MDC
Divisores
Múltiplos e divisores
27 exercícios de Matemática Básica

Faça também nosso Simulado Enem de Matemática

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.

Que tal um up?

Corretor de Redação
para o Enem Ferramenta Inteligente com feedback instantâneo

Exercícios exclusivos Acesso a centenas de questões com gabaritos

Estude sem publicidade Navegação limpa e focada para evitar distrações