Exercícios sobre velocidade angular (com gabarito respondido e explicado)
A velocidade angular é a grandeza física que indica a rapidez com que um corpo realiza um movimento de rotação, sendo definida pela razão entre o ângulo percorrido e o intervalo de tempo, geralmente expressa em radianos por segundo.
Nesta lista de exercícios, você poderá praticar esse conceito por meio de situações do cotidiano, com questões resolvidas e gabarito explicado, facilitando a compreensão do movimento circular e de suas principais relações.
Questão 1
João trabalha como técnico de manutenção em um parque de diversões e precisa verificar o funcionamento de uma roda-gigante antes da abertura do parque.
Segundo o manual do fabricante, a roda-gigante deve completar exatamente 3 voltas a cada 6 minutos para garantir a segurança e o conforto dos passageiros.
Utilizando um cronômetro, João confirmou que a roda-gigante está funcionando conforme as especificações do fabricante.
Satisfeito com o resultado, ele decidiu calcular a velocidade angular do brinquedo para incluir essa informação no relatório de manutenção.
Considerando que a roda-gigante opera de acordo com as especificações do fabricante e adotando π = 3,14, a velocidade angular desse brinquedo, em rad/s, é aproximadamente igual a:
a) 0,052 rad/s
b) 0,105 rad/s
c) 0,314 rad/s
d) 0,524 rad/s
Resposta correta: alternativa a) 0,052 rad/s.
Vamos resolver essa questão em dois passos. Mas, antes, vamos identificação os dados trazidos no enunciado do problema.
- Número de voltas: n = 3 voltas
- Tempo total: t = 6 minutos
Essa questão pode ser resolvida usando a definição de velocidade angular ou a frequência do movimento. Vamos resolvê-la pela definição de velocidade angular.
Passo 1: Vamos primeiro converter as unidades para o Sistema Internacional, ou seja, vamos converter o tempo para segundos e o número de voltas para radianos:
t = 6 min = 6 min . 60 = 360 s
Uma volta completa corresponde a um ângulo de 2π radianos. Portanto, 3 voltas completas serão:
Δθ = 3 . 2π = 6π rad
Passo 2: Agora podemos calcular a velocidade angular, lembrando que a velocidade angular (ω) é definida como a razão entre o deslocamento angular e o tempo:
ω = Δθ / Δt
Substituindo os valores, temos:
ω = 6π / 360
ω = (6 . 3,14) / 360
ω = 18,84 / 360
ω = 0,0523 rad/s
Arredondando ficamos com:
ω ≈ 0,052 rad/s
Questão 2
Durante um festival na cidade, foi instalada uma roda-gigante que gira com movimento uniforme.
Observando o funcionamento, um estudante de Física percebeu que a roda-gigante completa 3 voltas completas em 2 minutos.
Considere que o movimento é uniforme e que cada volta corresponde a uma rotação completa em torno do eixo.
Com base nesses dados, a velocidade angular da roda-gigante, em rad/s, e a frequência são respectivamente:
a) 0,05 rad/s e 0,008 voltas/s
b) 0,10 rad/s e 0,016 voltas/s
c) 0,16 rad/s e 0,025 voltas/s
d) 0,30 rad/s e 0,048 voltas/s
Resposta correta: alternativa c) 0,16 rad/s e 0,025 voltas/s.
Primeiro vamos organizar os dados trazidos no enunciado. Temos:
- número de voltas completas = 3
- tempo para dar as 3 voltas = 2 min = 2 . 60 = 120 s
Agora vamos expressar as voltas para radianos. Lembre que 1 volta completa equivale a 2π radianos. Assim:
Δθ = número de voltas . 2π
Δθ = 3. 2 . 3,14 = 18,84 rad
Agora podemos calcular a velocidade angular. Lembre que ela é definida como a relação do ângulo total percorrido pelo tempo gasto, ou:
ω = Δθ / Δt
ω = 18,84 / 120 = 0,157 rad/s
Tendo a velocidade angular podemos determinar a frequência usando a relação entre elas:
ω = 2π . f
f = ω / 2π
Assim:
f = 0,157 / 2π = 0,025 voltas/s
Questão 3
Em uma aula sobre energias renováveis, a professora de Física levou os alunos para observar um aerogerador (turbina eólica) instalado próximo à escola.
Ela explicou que as pás do aerogerador giram devido à força do vento, convertendo energia cinética em energia elétrica.
Utilizando um aplicativo de medição em seu tablet, a professora registrou que as pás do aerogerador estavam realizando 15 rotações por minuto (rpm) naquele momento.
Para contextualizar o conteúdo de cinemática angular, ela propôs aos alunos o seguinte desafio: calcular a velocidade angular das pás do aerogerador.
Considerando os dados fornecidos e adotando π = 3, a velocidade angular das pás do aerogerador, em rad/s, é igual a:
a) 0,25 rad/s
b) 0,50 rad/s
c) 1,00 rad/s
d) 1,50 rad/s
Resposta correta: alternativa d) 1,50 rad/s.
A velocidade angular (ω) mede a rapidez com que um objeto realiza uma rotação. Ela é definida pela razão entre o ângulo percorrido por unidade de tempo e é expressa em radianos por segundo.
O enunciado trouxe o valor da frequência de rotação das pás:
Frequência de rotação: f = 15 rpm (rotações por minuto)
Primeiro vamos converter a frequência para rotações por segundo ou Hz:
f = 15 rpm = 15 rotações / 1 minuto
f = 15 rotações / 60 segundos
f = 0,25 rotações/s = 0,25 Hz
Vamos agora aplicar a fórmula que relaciona a velocidade angular e a frequência:
ω = 2π . f
Onde:
- ω = velocidade angular (rad/s)
- π = 3 (valor adotado no enunciado)
- f = frequência (Hz)
Substituindo os valores, ficamos com:
ω = 2 . 3 . 0,25
ω = 1,50 rad/s
Questão 4
Carlos trabalha como técnico de manutenção em uma fábrica de tecidos.
Uma de suas funções é verificar o funcionamento das máquinas de costura industriais, que operam em alta velocidade para garantir a produtividade da linha de produção.
Durante uma inspeção de rotina, Carlos utilizou um tacômetro (instrumento que mede rotações) e verificou que o motor de uma máquina de costura estava operando a 1.800 rotações por minuto (rpm).
Ele precisa registrar essa informação no relatório técnico, porém o sistema da fábrica exige que a velocidade angular seja informada em rad/s.
Adotando π = 3,14, a velocidade angular do motor da máquina de costura, em rad/s, é aproximadamente:
a) 30 rad/s
b) 60 rad/s
c) 94 rad/s
d) 188 rad/s
Resposta correta: alternativa d) 188 rad/s.
Primeiro vamos identificar os dados que o enunciado trouxe:
- Frequência de rotação: f = 1.800 rpm (rotações por minuto)
- Valor de π: 3,14
Vamos converter rpm para Hz, ou seja, para rotações por segundo que é a unidade usada para frequência no Sistema Internacional.
f = 1.800 rpm = 1.800 rotações / 1 min
f = 1.800 rotações / 60 segundos
f = 30 rotações/s = 30 Hz
Podemos agora calcular a velocidade angular utilizando a relação entre velocidade angular e frequência:
ω = 2π . f
Substituindo os valores:
ω = 2 . 3,14 . 30
ω = 188,4 rad/s
Arredondando ficamos com:
ω ≈ 188 rad/s
Questão 5
Em um parque de diversões, há um carrossel clássico com cavalinhos dispostos em duas fileiras circulares: uma fileira interna, a 2 metros do centro, e uma fileira externa, a 4 metros do centro.
O carrossel gira com velocidade angular constante, completando uma volta a cada 8 segundos.
Duas crianças, Ana e Beatriz, estão brincando no carrossel.
Ana escolheu um cavalinho na fileira interna, enquanto Beatriz está em um cavalinho na fileira externa.
Adotando π = 3, analise a situação e determine as velocidades tangenciais de Ana e Beatriz, respectivamente:
a) 1,0 m/s e 2,0 m/s
b) 1,5 m/s e 3,0 m/s
c) 2,0 m/s e 4,0 m/s
d) 3,0 m/s e 6,0 m/s
Resposta correta: alternativa b) 1,5 m/s e 3,0 m/s.
Primeiro vamos identificar os dados que o enunciado trouxe:
- Raio da fileira interna (Ana): R₁ = 2 m
- Raio da fileira externa (Beatriz): R₂ = 4 m
- Período do carrossel: T = 8 s
- Valor de π: 3
Vamos calcular a velocidade angular do carrossel. Atente que ela é a mesma para todos os pontos do carrossel, pois ele gira como um corpo rígido. Assim:
ω = 2π / T = (2 . 3) / 8 = 6 / 8 = 0,75 rad/s
Podemos agora calcular a velocidade tangencial de Ana e de Beatriz, usando a relação entre velocidade tangencial e angular:
v = ω . R
Para Ana temos:
v1 = 0,75 . 2 = 1,5 m/s
Para Beatriz ficamos com:
v2 = 0,75 . 4 = 3,0 m/s
Questão 6
Gabriel é ciclista profissional e está preparando sua bicicleta para uma competição.
Ele sabe que o desempenho depende de vários fatores, incluindo o tamanho das rodas.
A bicicleta de Gabriel possui rodas com 35 cm de raio.
Durante um treino em velocidade constante, Gabriel percebeu que suas rodas estavam girando com uma velocidade angular de 20 rad/s.
O técnico da equipe pediu que Gabriel calculasse a velocidade tangencial de um ponto na borda da roda, pois esse valor corresponde à própria velocidade de deslocamento da bicicleta em relação ao solo (considerando que não há deslizamento).
A velocidade da bicicleta de Gabriel, em m/s, é igual a:
a) 2,52 km/h
b) 12,6 km/h
c) 25,2 km/h
d) 50,4 km/h
Resposta correta: alternativa c) 25,2 km/h.
Primeiro vamos identificar os dados trazidos no enunciado:
- Raio da roda: R = 35 cm = 0,35 m
- Velocidade angular: ω = 20 rad/s
Vamos aplicar a relação entre velocidade tangencial e angular dada por:
v = ω . R
Substituindo os valores temos:
v = 20 . 0,35
v = 7,0 m/s
A velocidade tangencial de um ponto na borda da roda é 7,0 m/s.
Como não há deslizamento entre a roda e o solo, essa também é a velocidade de deslocamento da bicicleta.
Vamos converter a velocidade tangencial para km/h, que é a unidade usada nas alternativas:
v = 7,0 m/s . 3,6 = 25,2 km/h
Questão 7
Em uma aula de Física, o professor trouxe um antigo toca-discos de vinil para demonstrar conceitos de movimento circular.
Ele explicou que os discos de vinil podem girar em diferentes rotações, sendo as mais comuns 33 rpm (rotações por minuto) para LPs e 45 rpm para compactos.
O professor colocou um disco de vinil do tipo LP (33 rpm) no toca-discos.
O disco possui 15 cm de raio.
Em seguida, ele fez a seguinte pergunta aos alunos:
"Uma formiga está parada na borda do disco. Qual é a velocidade tangencial dessa formiga enquanto o disco gira?"
Adotando π = 3 e considerando que 33 rpm ≈ 0,55 rotações por segundo, a velocidade tangencial da formiga é aproximadamente:
a) 0,75 m/s
b) 0,50 m/s
c) 0,25 m/s
d) 0,15 m/s
Resposta correta: alternativa b) 0,50 m/s.
Primeiro vamos identificar os dados trazidos no enunciado:
- Raio do disco: R = 15 cm = 0,15 m
- Frequência de rotação: f = 33 rpm ≈ 0,55 Hz
- Valor de π: 3
Vamos calcular a velocidade angular, usando a fórmula:
ω = 2π . f
ω = 2 . 3 . 0,55
ω = 3,3 rad/s
Podemos agora calcular a velocidade tangencial a partir da relação:
v = ω . R
v = 3,3 . 0,15
v = 0,495 m/s
Arredondando ficamos com:
v ≈ 0,50 m/s
Questão 8
Durante a aula de Física, o professor Henrique levou os alunos ao laboratório para realizar um experimento com um ventilador de teto.
Ele explicou que o ventilador possui três velocidades de rotação e que as pás têm comprimentos diferentes dependendo do modelo.
Para a demonstração, o professor utilizou um ventilador cujas pás têm 40 cm de comprimento (medidos do centro até a ponta).
Na velocidade máxima, o ventilador opera a 180 rpm (rotações por minuto).
O professor então projetou no quadro a seguinte imagem esquemática:
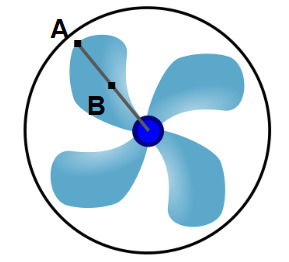
Onde:
- Ponto A: na ponta da pá a 40 cm do centro
- Ponto B: no meio da pá a 20 cm do centro
Após a explicação, o professor pediu que os alunos analisassem três afirmativas feitas por colegas da turma sobre o movimento das pás do ventilador.
Analise as afirmativas a seguir:
I. Os pontos A e B possuem a mesma velocidade angular, pois ambos completam uma volta no mesmo intervalo de tempo, já que fazem parte do mesmo corpo rígido (a pá do ventilador).
II. O ponto A possui maior velocidade tangencial que o ponto B, pois está mais afastado do eixo de rotação, e a velocidade tangencial é diretamente proporcional ao raio.
III. Se a frequência de rotação do ventilador for reduzida pela metade, a velocidade tangencial do ponto A também será reduzida pela metade, desde que o comprimento da pá permaneça o mesmo.
Está correto o que se afirma em:
a) I, apenas.
b) I e II, apenas.
c) II e III, apenas.
d) I, II e III.
Resposta correta: alternativa d) I, II e III.
Vamos analisar cada uma das afirmativas em separado.
Afirmativa I:
A velocidade angular (ω) representa a taxa de variação do ângulo em relação ao tempo. Em um corpo rígido, como a pá do ventilador, todos os pontos giram juntos, descrevendo o mesmo ângulo no mesmo intervalo de tempo.
Vamos calcular a velocidade angular do ventilador:
f = 180 rpm = 180 / 60 = 3 rotações / s = 3 Hz
ω = 2π . f = 2 . 3,14 . 3 ≈ 18,85 rad/s
Tanto o ponto A quanto o ponto B possuem ω = 18,85 rad/s, pois pertencem ao mesmo corpo rígido.
Portanto, a afirmativa está correta.
Afirmativa II:
A relação entre velocidade tangencial, velocidade angular e o raio é:
v = ω . R
Onde:
- v = velocidade tangencial (m/s)
- ω = velocidade angular (rad/s)
- R = distância ao eixo de rotação (m)
Para o ponto A, onde RA = 40 cm = 0,40 m, temos:
vA = 18,85 . 0,40 = 7,54 m/s
Para o ponto B que posssiu RB = 20 cm = 0,20 m, temos:
vB = 18,85 . 0,20 = 3,77 m/s
A afirmativa está correta porque vA > vB, já que RA > RB e ω é igual para ambos os pontos da pá.
Observação: A velocidade tangencial do ponto A é exatamente o dobro da velocidade do ponto B, pois o raio de A é o dobro do raio de B.
Afirmativa III:
A velocidade tangencial depende da velocidade angular e do raio:
v = ω . R
Como ω = 2π . f, podemos escrever:
v = 2π . f . R
Se o raio R permanecer constante e a frequência f for reduzida pela metade, ou:
f′ = f / 2
A nova velocidade tangencial será:
v′ = 2π . f′ . R = 2π . (f/2) . R = (2π . f . R) / 2 = v / 2
Vamos fazer uma verificação numérica:
- Frequência original: f = 3 Hz → vA = 7,54 m/s
Para a frequência reduzida: fʼ = 1,5 Hz teremos:
ωʼ = 2π . 1,5 = 9,42 rad/s
vA′ = 9,42 . 0,40 = 3,77 m/s
De fato, vAʼ = vA / 2, confirmando que a velocidade tangencial foi reduzida pela metade.
Portanto, a afirmativa está correta.
Logo, todas as afirmativas são corretas.
Para continuar praticando:
Exercícios sobre velocidade média (com gabarito explicado)
Exercícios sobre velocidade escalar média (com gabarito explicado)
Exercícios sobre velocidade vetorial média (com questões resolvidas e explicadas)
Exercícios sobre velocidade instantânea (com gabarito explicado)
SOUTO, Ana. Exercícios sobre velocidade angular (com gabarito respondido e explicado). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/exercicios-sobre-velocidade-angular-com-gabarito-respondido-e-explicado/. Acesso em:


