Velocidade instantânea: o que é e como calcular

A velocidade mostrada no velocímetro de um carro ou ônibus é chamada velocidade instantânea.

Ela difere da velocidade média porque é determinada como o deslocamento que ocorre em um único instante, por isso recebe o nome de instantânea.

Quando o motorista acelera o carro é possível ver no velocímetro o valor da velocidade aumentando. Quando ele pisa no freio, é possível observar o valor da velocidade diminuindo no velocímetro.

Vamos entender o que é a velocidade instantânea, sua relação com a velocidade média e como ela é determinada.

Cálculo da velocidade instantânea

A velocidade instantânea é definida da mesma forma que a velocidade média, ou seja, pela relação entre o deslocamento efetuado e tempo gasto, mas com a condição que o tempo gasto seja extremamente pequeno ou quase um instante.

Assim, temos:

A velocidade instantânea é definida, então, como a razão entre o deslocamento e o intervalo de tempo no limite em que o intervalo de tempo tende a zero.

Atente que não pode ser igual a zero porque teríamos uma divisão por zero!

A velocidade instantânea é determinada usando igual a 1 segundo, 0,5 segundo, 0,1 s ou 0,001 do segundo ou até mesmo tempos menores do que isso. Esse limite será dado pela qualidade e precisão do cronômetro usado para determiná-lo.

Velocidade instantânea e equação horária da velocidade

As equações horárias da velocidade para os movimentos são:

Movimento uniforme:

• v = v₀
• nesse caso a = 0 m/s², então v = v₀ = constante = velocidade média = velocidade instantânea

Movimento uniformemente variado:

• v = v₀ + a.t
• a = constante

Nesse caso a aceleração não é zero, e a equação permite determinar a velocidade em cada instante de tempo t.

Atente que no movimento uniformemente variado temos a velocidade inicial e a aceleração constantes. Assim, a equação horária da velocidade dá o valor da velocidade instantânea do objeto em cada tempo t.

Exemplo

Carlos ganhou um skate elétrico e está aprendendo a usá-lo em uma ciclovia reta e plana.

Em um determinado momento, ele está se movendo e, ao avistar um obstáculo, aciona os freios do skate.

A partir do instante em que os freios são acionados (vamos adotar como sendo o t = 0 s), a posição de Carlos (S), em metros, pode ser descrita pela função horária:

S(t) = 20t - 2,5t²

Considerando que a função descreve um movimento uniformemente variado, qual é a velocidade instantânea do skate de Carlos no instante t = 2 segundos após ele acionar os freios?
a) 5 m/s
b) 10 m/s
c) 15 m/s
d) 30 m/s

RESOLUÇÃO:

O objetivo é encontrar a velocidade instantânea em um tempo específico (t = 2s) a partir da função horária da posição.

Vamos resolver a questão em etapas:

1. Identificação dos parâmetros do movimento

A primeira coisa a fazer é comparar a função fornecida com a fórmula geral da posição para o Movimento Retilíneo Uniformemente Variado:

S(t) = S₀ + V₀t + (a/2)t²

Onde:

• S₀ é a posição inicial.
• V₀ é a velocidade inicial.
• a é a aceleração.

Comparando cada um dos termos com a função do exercício: S(t) = 20t - 2,5t², encontramos os seguintes valores:

• S₀ = 0 m pois consideramos o ponto de frenagem como a origem do espaço.
• V₀ = 20 m/s é a velocidade do skate no exato momento em que os freios são acionados, ou seja, no t = 0s.
• (a/2) = -2,5 termo que acompanha t² corresponde à metade da aceleração.

Podemos determinar a aceleração, fazendo:

a / 2 = -2,5

a = -2,5 . 2 = -5 m/s²

A aceleração é negativa, o que faz sentido, pois o skate está freando, ou seja, desacelerando.

2. Utilizando a função horária da velocidade

A fórmula geral para a velocidade instantânea no MUV é:

V(t) = V₀ + a.t

Agora, substituímos os valores de V₀ e a que já encontramos:

V(t) = 20 + (-5)t

V(t) = 20 - 5t

Essa é a função que nos dá a velocidade do skate em qualquer instante t, ou seja, a velocidade instantânea do skate.

3. Calculando a velocidade no instante desejado:

O exercício pede a velocidade instantânea no instante t = 2 s. Basta substituir t por 2 na função da velocidade:

V(2) = 20 - 5 . (2)

V(2) = 20 - 10

V(2) = 10 m/s

Portanto, 2 segundos após acionar os freios, a velocidade do skate é de 10 m/s.

CONCLUSÃO: a alternativa correta é a b) 10 m/s.

Velocidade instantânea e gráficos do movimento uniformemente variado

Os gráficos do espaço e da velocidade do movimento uniformemente variados possuem as seguintes formas:

Espaço ou posição (S) em função do tempo → parábola para cima ou para baixo:

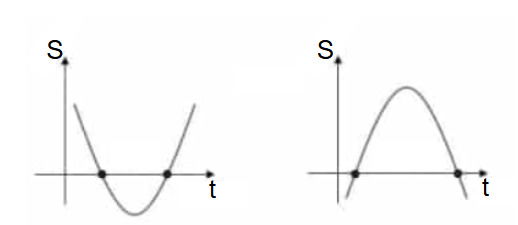
Nesse caso, a velocidade instantânea é igual à tangente da curva no instante desejado, conforme ilustrado abaixo:

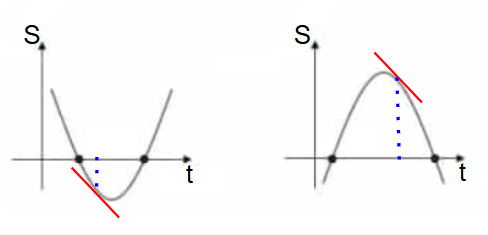
Para saber como determinar a tangente de curvas, veja Estudo das derivadas: introdução e regras gerais.

Velocidade (v) em função do tempo → reta crescente ou decrescente

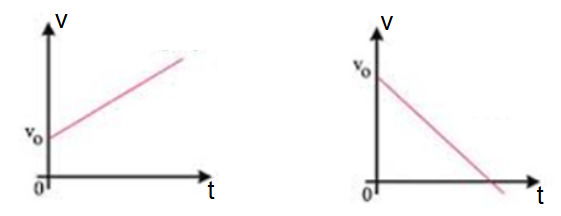
Nesse caso, o valor da velocidade instantânea é lida diretamente no gráfico considerando o instante desejado.

Exemplo

Mariana está visitando um prédio comercial moderno que possui um elevador panorâmico de alta velocidade.

Para entender a tecnologia, ela pesquisa e encontra um gráfico que descreve a velocidade (v) do elevador em função do tempo (t) durante uma subida entre dois andares, a partir do repouso.

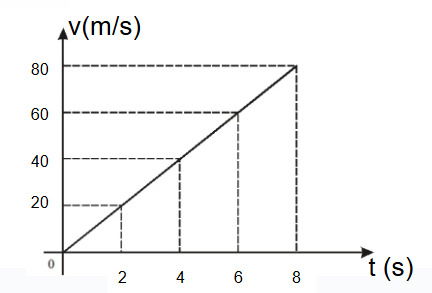
Analise o gráfico e responda: qual é a velocidade instantânea do elevador no instante t = 4 segundos?

Alternativas:
a) 15 m/s
b) 30 m/s
c) 40 m/s
d) 80 m/s

Resolução:

O valor da velocidade pode ser lido diretamente no gráfico a partir da linha tracejada em direção à reta da velocidade no instante 4s.

A velocidade instantânea é 40 m/s para o instante 4s.

Resposta correta: alternativa c).

Velocidades média e instantânea

Já sabemos que a velocidade média é definida como a razão entre um deslocamento e o tempo necessário para realizá-lo, ou seja:

Nesse caso não existe nenhuma restrição quanto ao valor do deslocamento ou do tempo.

Podemos determinar a velocidade média de uma viagem de 5 horas entre duas cidades que distam 400 km uma da outra aplicando diretamente a definição:

v_média = 400 km / 5 horas = 80 km/h

Mas a velocidade média não transmite o que aconteceu durante essas cinco horas, ou seja, ela não indica se o motorista parou durante um tempo para abastecer o carro e lanchar, se ele correu em alguns trechos da estrada, se teve que frear para passar nos pedágios, e assim por diante.

A velocidade média apenas nos diz que, se o motorista fizesse a viagem com velocidade constante de 80 km/h, ele demoraria exatamente as 5 horas para percorrer a distância de 400 km.

E quando queremos saber os detalhes da viagem como, por exemplo, qual foi a maior velocidade atingida durante a viagem?

Nesse caso temos que usar a velocidade instantânea, pois é ela que dá os detalhes da viagem.

Para praticar: Exercícios sobre velocidade instantânea (com gabarito explicado)