Exercícios sobre função logarítmica (com gabarito explicado)
A função logarítmica é um conteúdo fundamental da Matemática, com aplicações que vão da análise de gráficos a situações do cotidiano, como escalas de pH, decibéis e terremotos. Os exercícios seguintes são ideais para revisar conceitos, tirar dúvidas e aprofundar o entendimento do tema.
Questão 1
O domínio real mais amplo da função definida por é:
a)
b)
c)
d)
Aplicando a condição de existência para o logarítimo temos:
Fazendo a interseção entre as três condições temos como solução o intervalo:
Questão 2
Dada a função real a quantidade se soluções reais da equação
é:
a) 1
b) 2
c) 3
d) 4
Aplicando a condição de existência ao logaritmando temos:
Igualando a função a zero e aplicando a definição de logaritmo obtemos:
Como ambas são soluções da equação, portanto temos 2 soluções.
Questão 3
Observe o gráfico da função logarítmica abaixo:
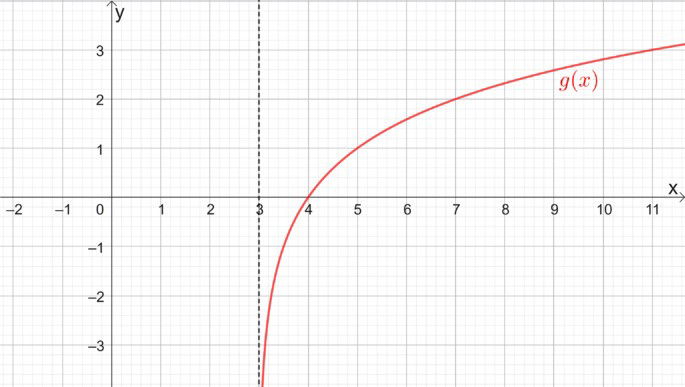
A função representada no gráfico pode ser definida como:
a)
b)
c)
d)
Observe que entre a assíntota vertical e a raiz temos um intervalo de uma unidade característico da função logarítimica . Vemos que o gráfico de
em relação à
é uma translação horizontal de 3 unidades para direita, ou seja,
.
A função é definida por que para
teremos
, para qualquer valor de b, portanto a única alternativa que satisfaz as condições é
.
Questão 4
Para quais valores de a função
é decrescente?
a)
b)
c)
d)
Quando a base também é uma função de x devemos proceder a análise efetuando a mudança de base.
Como o numerador é sempre constante e positivo, devemos analisar o comportamento do denominador, pois para que a função seja decrescente o denominador deve aumentar.
Logo,
aumenta para
e pela condição do logaritmando temos
efetuando a interseção teremos o seguinte intervalo:
, mas com cuidado na função original
.
Finalmente a função é decrescente em .
Questão 5
Na escala Richter, a magnitude de um terremoto é definida por:
em que é a intensidade do terremoto e
é uma intensidade de referência.
Dois terremotos A e B apresentam magnitudes 6,5 e 4,5, respectivamente. A razão entre as intensidades é:
a) 10
b) 100
c) 1000
d) 10000
A escala Richter é logarítmica de base 10. A diferença entre as magnitudes é:
6,5 − 4,5 = 2
Isso significa que a razão entre as intensidades é:
Questão 6
O de uma solução aquosa é definido por:
onde representa a concentração de íons hidrogênio, em mol/L.
Se o de uma solução aumenta de 3 para 5, então a concentração de íons
:
a) diminui 2 vezes
b) diminui 10 vezes
c) diminui 100 vezes
d) aumenta 100 vezes
Um aumento de uma unidade no corresponde a uma diminuição de 10 vezes na concentração de íons
.
Como o aumentou de 3 para 5, houve um aumento de 2 unidades. Portanto, a concentração diminuiu:
Questão 7
O nível sonoro , medido em decibéis (dB), é dado por:
em que é a intensidade do som e
é uma intensidade de referência.
Se a intensidade de uma fonte sonora é multiplicada por 100, o aumento no nível sonoro será de:
a) 10 dB
b) 20 dB
c) 30 dB
d) 100 dB
Quando a intensidade é multiplicada por 100, temos:
Logo:
Questão 8
Em um laboratório, o número de bactérias , em função do tempo
(em horas), é modelado por:
Deseja-se determinar o tempo necessário para que o número inicial de bactérias triplique.
Dado: .
O valor de , em horas, é aproximadamente:
a) 3,3
b) 2,5
c) 2,0
d) 1,6
Triplicar o número inicial de bactérias significa que:
Como:
Continue praticando: Exercícios de Logaritmo: questões resolvidas e comentadas
Referências Bibliográficas
CANELLAS, William. Matemática para o infinito e além: volume 2. 1. ed. Joinville: Clube de Autores, 2023.
DANTE, Luiz Roberto. Matemática: contexto e aplicações. Volume 2. 3. ed. São Paulo: Ática, 2019.
IEZZI, Gelson; DOLCE, Osvaldo; DEGENSZTAJN, David; PÉRIGO, Roberto. Matemática: ciência e aplicações. Volume 2. 9. ed. São Paulo: Saraiva, 2018.
PAIVA, Manoel Rodrigues. Matemática: volume único. 3. ed. São Paulo: Moderna, 2015.
CANELLAS, William. Exercícios sobre função logarítmica (com gabarito explicado). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/exercicios-sobre-funcao-logaritmica-com-gabarito-explicado/. Acesso em:


