Paralelepípedo: fórmulas e exercícios
O Paralelepípedo é uma figura geométrica espacial que faz parte dos sólidos geométricos.
Trata-se de um prisma que possui base e faces em formato de paralelogramos (polígono de quatro lados).
Em outras palavras, o paralelepípedo é um prisma quadrangular com base de paralelogramos.
Faces, Vértices e Arestas do paralelepípedo
O paralelepípedo possui:
- 6 faces (paralelogramos)
- 8 vértices
- 12 arestas
Classificação do paralelepípedo
De acordo com a perpendicularidade de suas arestas em relação a base, os paralelepípedos são classificados em:
Paralelepípedos Oblíquos: possuem arestas laterais oblíquas à base.
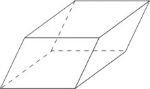
Paralelepípedos Reto: possuem arestas laterais perpendiculares à base, ou seja, apresentam ângulos retos (90º) entre cada uma das faces.
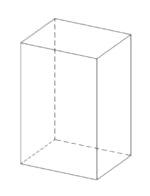
Lembre-se que o paralelepípedo é um sólido geométrico, ou seja, uma figura com três dimensões (altura, largura e comprimento).
Todos os sólidos geométricos são formados pela união de figuras planas. Para exemplificar melhor, confira abaixo a planificação do paralelepípedo reto:

Fórmulas do paralelepípedo
Segue abaixo as principais fórmulas do paralelepípedo, onde a, b e c são as arestas do paralelogramo:
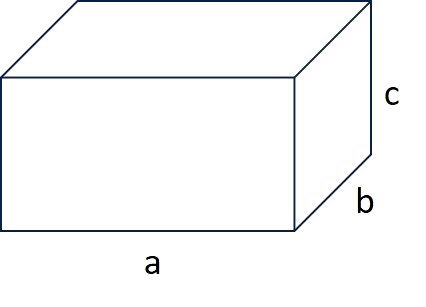
Área da Base
Área Total
Volume
Diagonais
Fique Atento!
Os paralelepípedos retângulos são prismas retos que apresentam base e face retangulares.
Um caso especial de paralelepípedo retângulo é o cubo, figura geométrica com seis faces quadrangulares. Para calcular a área lateral de um paralelepípedo retângulo utiliza-se a fórmula:
Donde, a, b e c são arestas da figura.
Para complementar sua pesquisa sobre o tema, veja também:
Exercícios de paralelepípedo resolvidos
Segue abaixo dois exercícios de paralelepípedo que caíram no Enem:
Exercício 1
(Enem 2010) A siderúrgica “Metal Nobre” produz diversos objetos maciços utilizando o ferro. Um tipo especial de peça feita nessa companhia tem o formato de um paralelepípedo retangular, de acordo com as dimensões indicadas na figura que segue

O produto das três dimensões indicadas na peça resultaria na medida da grandeza:
a) massa
b) volume
c) superfície
d) capacidade
e) comprimento
Exercício 2
(Enem 2010) Uma fábrica produz barras de chocolates no formato de paralelepípedos e de cubos, com o mesmo volume. As arestas da barra de chocolate no formato de paralelepípedo medem 3 cm de largura, 18 cm de comprimento e 4 cm de espessura.
Analisando as características das figuras geométricas descritas, a medida das arestas dos chocolates que têm o formato de cubo é igual a:
a) 5 cm
b) 6 cm
c) 12 cm
d) 24 cm
e) 25 cm
GOUVEIA, Rosimar. Paralelepípedo: fórmulas e exercícios. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/paralelepipedo/. Acesso em:



