Cone

Rosimar Gouveia

Professora de Matemática e Física

Cone é um sólido geométrico que faz parte dos estudos da geometria espacial.

Ele possui uma base circular (r) formada por segmentos de reta que têm uma extremidade num vértice (V) em comum.

Além disso, o cone possui a altura (h), caracterizada pela distância do vértice do cone ao plano da base.

Possui também a denominada geratriz, ou seja, a lateral formada por qualquer segmento que tenha uma extremidade no vértice e a outra na base do cone.

Classificação dos Cones

Os cones, dependendo da posição do eixo em relação à base, são classificados em:

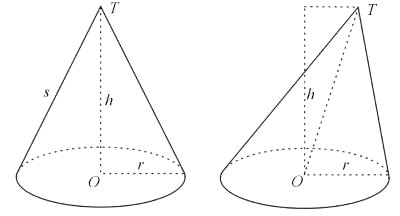
• Cone Reto: No cone reto, o eixo é perpendicular à base, ou seja, a altura e o centro da base do cone formam um ângulo de 90º, donde todas as geratrizes são congruentes entre si e, de acordo com o Teorema de Pitágoras, tem-se a relação: g²=h²+r². O cone reto é também chamado de “cone de revolução” obtido pela rotação de um triângulo em torno de um de seus catetos.
• Cone Oblíquo: No cone oblíquo, o eixo não é perpendicular à base da figura.

Observe que o chamado “cone elíptico” possui base elíptica e pode ser reto ou oblíquo.

Para compreender melhor a classificação dos cones, observe as figuras abaixo:

Fórmulas do Cone

Segue abaixo as fórmulas para encontrar as áreas e o volume do cone:

Áreas do Cone

Área da Base: Para calcular a área da base de um cone (circunferência), utiliza-se a seguinte fórmula:

A_b = п.r²

Donde:

A_b: área da base
п (Pi) = 3,14
r: raio

Área Lateral: formada pela geratriz do cone, a área lateral é calculada através da fórmula:

A_l = п.r.g

Donde:

A_l: área lateral
п (PI) = 3,14
r: raio
g: geratriz

Área Total: para calcular a área total do cone, soma-se a área da lateral e a área da base. Para isso utiliza-se a seguinte expressão:

A_t = п.r (g+r)

Donde:

A_t: área total
п = 3,14
r: raio
g: geratriz

Volume do Cone

O volume do cone corresponde a 1/3 do produto da área da base pela altura, calculado pela seguinte fórmula:

V = 1/3 п.r². h

Donde:

V = volume
п = 3,14
r: raio
h: altura

Para saiba mais, leia também:

Exercício Resolvido

Um cone circular reto tem raio da base de 6 cm e uma altura de 8 cm. Segundo os dados oferecidos, calcule:

1. a área da base
2. a área lateral
3. a área total

Veja também:

• Corpos redondos
• Fórmulas de Matemática
• Cônicas
• Sólidos Geométricos
• Exercícios de cone

Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.