Cilindro

Rosimar Gouveia

Professora de Matemática e Física

O cilindro ou cilindro circular é um sólido geométrico alongado e arredondado que possui o mesmo diâmetro ao longo de todo o comprimento.

Essa figura geométrica, que faz parte dos estudos de geometria espacial, apresenta dois círculos com raios de medidas equivalentes os quais estão situados em planos paralelos.

Componentes do Cilindro

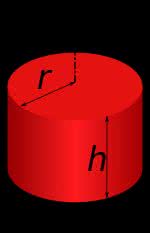
• Raio: distância entre o centro do cilindro e a extremidade.
• Base: plano que contém a diretriz e no caso dos cilindros são duas bases (superior e inferior).
• Geratriz: corresponde à altura (h=g) do cilindro.
• Diretriz: corresponde à curva do plano da base.

Classificação dos Cilindros

Dependendo da inclinação do eixo, ou seja, do ângulo formado pela geratriz, os cilindros são classificados em:

Cilindro Reto: Nos cilindros circulares retos, a geratriz (altura) está perpendicular ao plano da base.

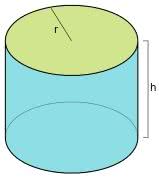
Cilindro Oblíquo: Nos cilindros circulares oblíquos, a geratriz (altura) está oblíqua ao plano da base.

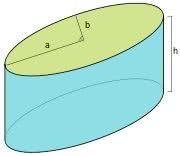
O chamado “cilindro equilátero” ou “cilindro de revolução” é caracterizado pela mesma medida do diâmetro da base e da geratriz (g=2r). Isso porque sua seção meridiana corresponde a um quadrado.

Para ampliar seus conhecimentos sobre o tema, veja outras figuras que fazem parte da Geometria Espacial.

Fórmulas do Cilindro

Segue abaixo as fórmulas para calcular as áreas e o volume do cilindro:

Áreas do Cilindro

Área da Base: Para calcular a área da base do cilindro, utiliza-se a seguinte fórmula:

A_b= π.r²

Onde:

Ab: área da base
π (Pi): 3,14
r: raio

Área Lateral: Para calcular a área lateral do cilindro, ou seja, a medida da superfície lateral, utiliza-se a fórmula:

A_l= 2 π.r.h

Onde:

A_l: área lateral
π (Pi): 3,14
r: raio
h: altura

Área Total: Para calcular a área total do cilindro, ou seja, a medida total da superfície da figura, soma-se 2 vezes a área da base à área lateral, a saber:

A_t= 2.A_b+A_l ou A_t = 2(π.r²) + 2(π.r.h)

Onde:

A_t: área total
A_b: área da base
A_l: área lateral
π (Pi): 3,14
r: raio
h: altura

Volume do Cilindro

O volume do cilindro é calculado a partir do produto da área da base pela altura (geratriz):

V = A_b.h ou V = π.r².h

Onde:

V: volume
A_b: área da base
π (Pi): 3,14
r: raio
h: altura

Exercícios Resolvidos

Para compreender melhor o conceito de cilindro, confira abaixo dois exercícios, sendo que um deles caiu no ENEM:

1. Uma lata em forma de cilindro equilátero tem altura de 10 cm. Calcule a área lateral, a área total e o volume desse cilindro.

2. (ENEM-2011) É possível usar água ou comida para atrair as aves e observá-las. Muitas pessoas costumam usar água com açúcar, por exemplo, para atrair beija-flores, mas é importante saber que, na hora de fazer a mistura, você deve sempre usar uma parte de açúcar para cinco partes de água. Além disso, em dias quentes, precisa trocar a água de duas a três vezes, pois com o calor ela pode fermentar e, se for ingerida pela ave, pode deixá-la doente. O excesso de açúcar, ao cristalizar, também pode manter o bico da ave fechado, impedindo-a de se alimentar. Isso pode até matá-la.

Ciência Hoje das crianças. FNDE; Instituto Ciência Hoje, ano 19, n. 166, mar. 1996.

Pretende-se encher completamente um copo com a mistura para atrair beija-flores. O copo tem formato cilíndrico, e suas medidas são 10 cm de altura e 4 cm de diâmetro. A quantidade de água que deve ser utilizada na mistura é cerca de (utilize π(pi) = 3)

a) 20 mL.
b) 24 mL.
c) 100 mL.
d) 120 mL.
e) 600 mL.

Pratique com 13 exercícios sobre cilindros.

Leia também:

• Corpos redondos
• Formas Geométricas
• Sólidos Geométricos
• Número Pi
• Fórmulas de Matemática
• Paralelepípedo

Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.