Pirâmide

Rafael C. Asth

Professor de Matemática e Física

A pirâmide é uma figura geométrica espacial, mais precisamente um poliedro.

Ela é composta por uma base e um vértice. Sua base é um polígono e pode ser: triangular, pentagonal, quadrada, retangular, paralelogramo ou outras.

Já o vértice, corresponde ao ponto mais distante da base da pirâmide e une todas as faces laterais triangulares.

Em outros termos, a pirâmide é um sólido geométrico de base poligonal que possui todos os vértices num plano (plano da base). Sua altura corresponde a distância entre o vértice da pirâmide e sua base.

Observe que o número de lados do polígono da base corresponde ao número de faces laterais da pirâmide.

Tipos de Pirâmide

Segundo as bases e o número arestas que formam as pirâmides, elas são classificadas em:

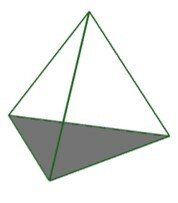
Pirâmide Triangular: sua base é um triângulo, composta de quatro faces: três faces laterais e a face da base.

Pirâmide de base triangular.

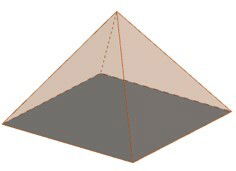
Pirâmide Quadrangular: sua base é um quadrado, composta de cinco faces: quatro faces laterais e a face da base.

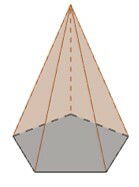
Pirâmide Pentagonal: sua base é um pentágono, composta de seis faces: cinco faces laterais e a face da base.

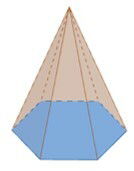
Pirâmide Hexagonal: sua base é um hexágono, composta de sete faces: seis faces laterais e face da base.

No tocante à inclinação da base, as pirâmides são classificadas de duas maneiras:

Pirâmides Retas, que formam um ângulo de 90º;
Pirâmides Oblíquas, que apresentam ângulos diferentes de 90º.

Elementos da Pirâmide

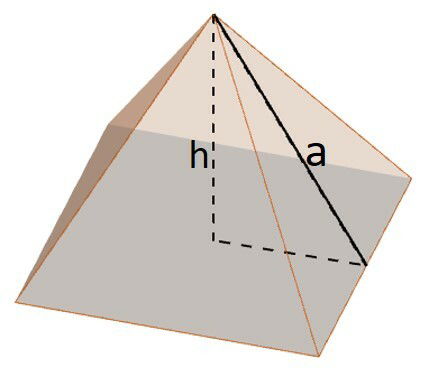
Base: corresponde à região plana poligonal em que se sustenta a pirâmide.

Altura (h): designa a distância do vértice da pirâmide ao plano da base.

Arestas: são classificadas em arestas da base, ou seja, todos os lados do polígono da base, e arestas laterais, segmentos formados pela distância do vértice da pirâmide até sua base.

Apótemas (a): corresponde à altura de cada face lateral, ou seja, é um segmento que liga o vértice da pirâmide à sua base, fazendo um ângulo de 90º.

Superfície lateral: É a superfície poliédrica composta por todas as faces laterais da pirâmide.

Superfície total: É a superfície composta da área lateral mais a área da base.

Área da Pirâmide

Para calcular a área total da pirâmide, utiliza-se a seguinte fórmula:

$começar estilo tamanho matemático 16px Área espaço total dois pontos espaço reto A com reto L subscrito mais espaço reto A com reto b subscrito fim do estilo$

Onde,

Área lateral $reto A com reto L subscrito$

É a soma das áreas de todas as faces laterais. Como as laterais são sempre triângulos, a área de uma lateral é calculada por:

$reto A com reto L subscrito igual a abre parênteses numerador reto b espaço. espaço reto h sobre denominador 2 fim da fração fecha parênteses$

A base b de uma lateral é igual ao lado da base e a altura h igual ao apótema lateral da pirâmide.

No caso particular da base ser um polígono regular:

$reto A com reto L subscrito igual a reto n. abre parênteses numerador reto b espaço. espaço reto h sobre denominador 2 fim da fração fecha parênteses$

Em que n é o número de lados da base e multiplica a área dos triângulos laterais.

Área da base $reto A com reto b subscrito$

O cálculo da área da base depende do polígono que forma a base. Por exemplo, se a base possuir a forma de um:

$Triângulo dois pontos espaço espaço reto A com reto b subscrito igual a numerador reto b espaço. espaço reto h sobre denominador 2 fim da fração Quadrado dois pontos espaço reto A com reto b subscrito espaço igual a espaço reto L ² espaço Retângulo dois pontos espaço reto A com reto b subscrito espaço igual a espaço largura espaço. espaço comprimento$

As áreas são sempre expressas em medidas quadradas, como cm² e m².

Volume da Pirâmide

Para calcular o volume da pirâmide, tem-se a equação:

$começar estilo tamanho matemático 18px reto V igual a numerador Ab. reto h sobre denominador 3 fim da fração espaço fim do estilo$

Onde:

A_b: Área da base
h: altura

O volume é expresso em unidade cúbicas, como cm³ e m³.