Volume do cone: fórmulas e exercícios

O volume do cone é calculado pelo produto entre a área da base e a medida da altura, e o resultado dividido por três.

Lembre-se que o volume significa a capacidade que possui uma figura geométrica espacial.

Confira alguns exemplos nesse artigo, exercícios resolvidos e testes de vestibular.

Fórmula do Volume do Cone

A fórmula para calcular o volume do cone é:

Onde:

V: volume
π: constante que equivale a 3,14 aproximadamente
r: raio
h: altura

Atenção!

O volume de uma figura geométrica é sempre calculado em m³, cm³, etc.

Exemplo

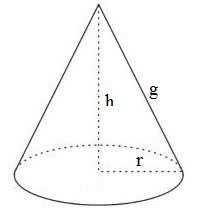
Calcule o volume de um cone circular reto cujo raio da base mede 3 m e geratriz 5 m.

Resolução

Primeiramente, devemos calcular a altura do cone. Nesse caso, podemos utilizar o teorema de Pitágoras:

h² + r² = g²
h² + 9 = 25
h² = 25 – 9
h² = 16
h = 4 m

Após encontrar a medida da altura, basta inserir na fórmula do volume:

V = 1/3 π.r². h
V = 1/3 π . 9 . 4
V = 12 π m³

Entenda mais sobre o Teorema de Pitágoras.

Volume do Tronco do Cone

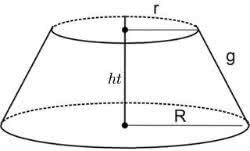
Se cortamos o cone em duas partes, teremos a parte que contém o vértice e a parte que contém a base.

O tronco do cone é a parte mais larga do cone, ou seja, o sólido geométrico que contém a base da figura. Ele não inclui a parte que contém o vértice.

Assim, para calcular o volume do tronco do cone, utiliza-se a expressão:

Onde:

V: volume do tronco do cone
π: constante que equivale a 3,14 aproximadamente
h: altura
R: raio da base maior
r: raio da base menor

Exemplo

Calcule o tronco do cone cujo raio da base maior mede 20 cm, o raio da base menor mede 10 cm e a altura é de 12 cm.

Resolução

Para encontrar o volume do tronco do cone basta colocar os valores na fórmula:

R: 20 cm
r: 10 cm
h: 12 cm

V = π.h/3 . (R² + R . r +r²)
V = π.12/3 . (400 + 200 + 100)
V = 4п . 700
V = 2800 π cm³

Continue sua pesquisa. Leia os artigos:

• Cone
• Área do Cone
• Geometria Espacial
• Volume do Cilindro

Exercícios de volume do cone

Exercício 1

(Cefet- SC) Dado um copo em forma de cilindro e outro de forma cônica de mesma base e altura. Se eu encher completamente o copo cônico com água e derramar toda essa água no copo cilíndrico, quantas vezes terei que fazê-lo para encher completamente esse copo?

a) Apenas uma vez.
b) Duas vezes.
c) Três vezes.
d) Uma vez e meia.
e) É impossível saber, pois não se sabe o volume de cada sólido.

Exercício 2

(PUC-MG) Um monte de areia tem a forma de um cone circular reto, com volume V= 4пm³. Se o raio da base é igual a dois terços da altura desse cone, pode-se afirmar que a medida da altura do monte de areia, em metros, é:

a) 2
b) 3
c) 4
d) 5

Exercício 3

(PUC-RS) O raio da base de um cone circular reto e a aresta da base de uma pirâmide quadrangular regular têm mesma medida. Sabendo que suas alturas medem 4 cm, então a razão entre o volume do cone e o da pirâmide é:

a) 1
b) 4
c) 1/п
d) п
e) 3п

Exercício 4

(Cefet-PR) O raio da base de um cone circular reto mede 3 m e o perímetro de sua seção meridiana mede 16 m. O volume desse cone mede:

a) 8п m³
b) 10п m³
c) 14п m³
d) 12п m³
e) 36п m³

Exercício 5

(UF-GO) A terra retirada na escavação de uma piscina semicircular de 6 m de raio e 1,25 m de profundidade foi amontoada, na forma de um cone circular reto, sobre uma superfície horizontal plana. Admita que a geratriz do cone faça um angulo de 60° com a vertical e que a terra retirada tenha volume de 20% maior do que o volume da piscina. Nessas condições, a altura do cone, em metros, é de:

a) 2,0
b) 2,8
c) 3,0
d) 3,8
e) 4,0

Exercícios de cone