Prisma triangular: características e como calcular (com fórmulas e exemplos)

Um prisma triangular é um sólido geométrico (poliedro) que possui:

• 2 bases triangulares paralelas e congruentes (iguais);
• 3 faces laterais em forma de paralelogramo (ou retângulo, nos prismas retos);
• 9 arestas (3 em cada base + 3 laterais);
• 6 vértices (3 em cada base).

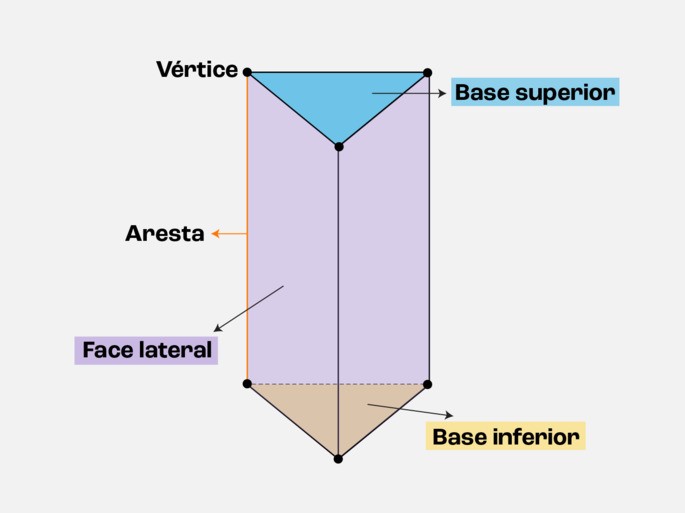
As bases são os dois triângulos. Uma base fica em cima e outra embaixo (ou nas extremidades, dependendo da posição).

As faces laterais são as "paredes" que conectam as bases. Como o triângulo tem 3 lados, precisamos de 3 faces para conectar uma base à outra.

Assim, o prisma triangular possui 5 faces totais: 2 bases + 3 laterais.

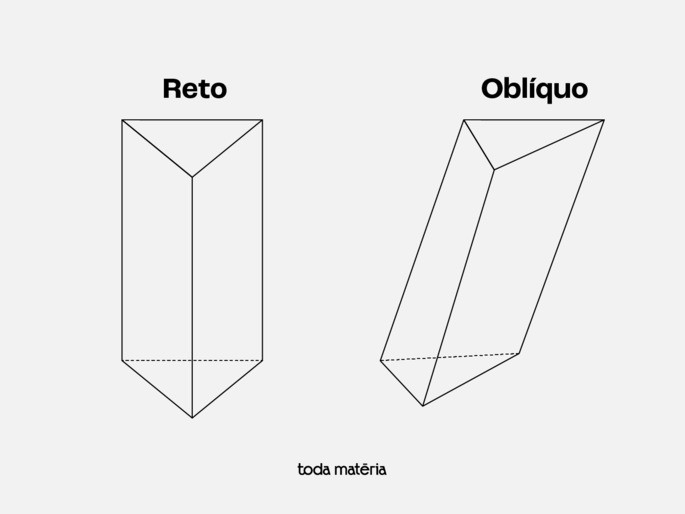
Se o prisma é reto, está "em pé" (perpendicular às bases), as faces laterais são retângulos.

Se o prisma é oblíquo, está "inclinado", as faces laterais são paralelogramos inclinados (não retângulos).

Elementos do prisma triangular

Elemento	Quantidade	Descrição
Bases	2	Triângulos idênticos e paralelos
Faces Laterais	3	Paralelogramos (retângulos se for reto)
Arestas das Bases	6	Lados dos triângulos (3+3)
Arestas Laterais	3	Linhas que conectam as bases
Total de Arestas	9	Todas as "linhas" do prisma
Vértices	6	Todos os "cantos" (3+3)

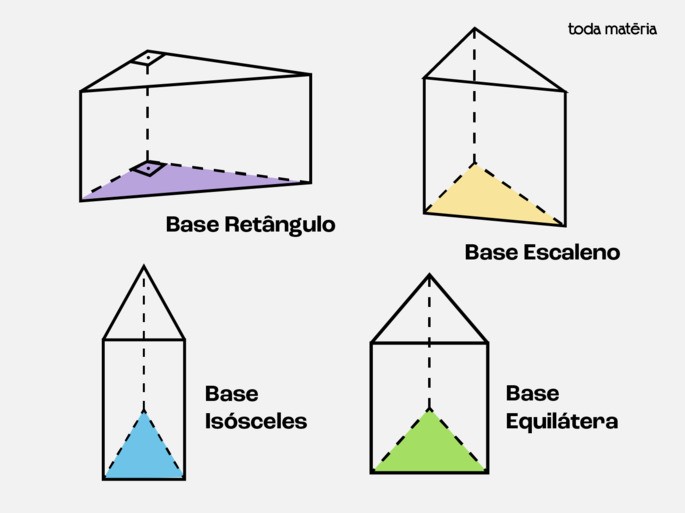
Classificação dos prismas triangulares em relação às bases

Os triângulos das bases podem ser: equilátero, isósceles, escaleno ou retângulo.

Área da Base (Ab)

A área da base depende do tipo de triângulo. As fórmulas mais comuns são:

Onde:

• b = base do triângulo
• h_triângulo = altura do triângulo

Para Triângulo Equilátero (lado L):

Área Lateral (AL)

A área lateral é a soma das áreas das três faces laterais.

Para Prisma Reto:

Onde:

• a, b, c = lados do triângulo da base
• h = altura do prisma

Área Total (At)

A área total é a soma das áreas das bases e das faces laterais.

Volume (V)

O volume representa o espaço ocupado pelo prisma.

Para calcular o volume de um prisma qualquer, multiplicamos o valor da área da base pela altura do prisma.

Onde, Ab é a área da base e h a altura.

Exercícios sobre prismas triangulares

Exercício 1

Um prisma triangular reto tem base com lados 3 cm, 4 cm e 5 cm (triângulo retângulo). A altura do prisma é 8 cm. Calcule o volume.

Exercício 2

Um prisma triangular tem base equilátera de lado 10 cm e altura 20 cm. Calcule a área total.

Exercício 3

Um prisma triangular tem volume de 300 cm³ e área da base de 25 cm². Qual é a altura do prisma?

Veja também:

• Prisma: elementos, classificação, fórmulas e exercícios
• Volume do Prisma: fórmula e exercícios
• Exercícios sobre o volume do prisma
• Sólidos Geométricos: exemplos, nomes e planificação
• Exercícios de Geometria Espacial (com questões resolvidas)