Plano Inclinado

Rafael C. Asth

Professor de Matemática e Física

O plano inclinado é uma superfície plana, elevada e inclinada, por exemplo, uma rampa.

Na física, estudamos o movimento dos objetos bem como a aceleração e as forças atuantes que ocorrem num plano inclinado.

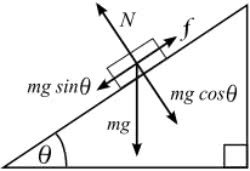
Plano Inclinado sem Atrito

Existem 2 tipos de forças que atuam nesse sistema sem atrito: a força normal, que faz 90º em relação ao plano, e a força peso (força vertical para baixo). Note que elas possuem direções e sentidos diferentes.

A força normal atua perpendicularmente à superfície de contato.

Para calcular a força normal numa superfície plana horizontal, utiliza-se a fórmula:

Sendo,

N: força normal
m: massa do objeto
g: gravidade

Já a força peso, atua em virtude da força da gravidade que “puxa” todos os corpos da superfície em direção ao centro da Terra. Ela é calculada pela fórmula:

Onde:

P: força peso
m: massa
g: aceleração da gravidade

Plano Inclinado com Atrito

Quando há o atrito entre o plano e o objeto temos mais uma força atuante: a força atrito.

Para calcular a força atrito utiliza-se a expressão:

Onde:

F_at: força de atrito
µ: coeficiente de atrito
N: força normal

A fórmula da força normal N, no plano inclinado é:

Pois, a força N é igual em valor a componente do peso nesta direção.

Obs: O coeficiente de atrito (µ) dependerá do material de contato entre os corpos e sua condição.

Aceleração no Plano Inclinado

No plano inclinado há uma altura correspondente a elevação da rampa e um ângulo formado em relação à horizontal.

Nesse caso, a aceleração do objeto é constante devido as forças atuantes: peso e a normal.

Para determinar o valor da aceleração num plano inclinado, precisamos encontrar a força resultante, decompondo a força peso em dois planos (x e y).

Logo, as componentes da força peso:

P_x: perpendicular ao plano
P_y: paralelo ao plano

Para encontrar a aceleração no plano inclinado sem atrito, utiliza-se as relações trigonométricas do triângulo retângulo:

P_x = P . sen θ
P_y = P . cos θ

De acordo com a segunda Lei de Newton:

F = m . a

Onde,

F: força
m: massa
a: aceleração

Logo,

P_x = m .a
P . sen θ = m .a
m . g . sen θ = m .a
a = g . sen θ

Assim, temos a fórmula da aceleração utilizada no plano inclinado sem atrito, a qual não dependerá da massa do corpo.

Exercícios de Vestibular com Gabarito

Questão 1

(UNIMEP-SP) Um bloco de massa 5kg é arrastado ao longo de um plano inclinado sem atrito, conforme a figura.

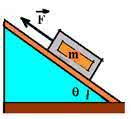
Para que o bloco adquira uma aceleração de 3m/s² para cima, a intensidade da F deverá ser: (g = 10m/s², sen θ = 0,8 e cos θ = 0,6).

a) igual ao peso do bloco

b) menor que o peso do bloco

c) igual à reação do plano

d) igual a 55N

e) igual a 10N

Questão 2

(UNIFOR-CE) Um bloco de massa de 4,0 kg é abandonado num plano inclinado de 37º com a horizontal com o qual tem coeficiente de atrito 0,25. A aceleração do movimento do bloco é em m/s². Dados: g = 10 m/s²; sen 37º = 0,60; cos 37º = 0,80.

a) 2,0

b) 4,0

c) 6,0

d) 8,0

e) 10

Questão 3

(Vunesp) No plano inclinado da figura abaixo, o coeficiente de atrito entre o bloco A e o plano vale 0,20. A roldana é isenta de atrito e despreza-se o efeito do ar.

Os blocos A e B têm massas iguais a m cada um e a aceleração local da gravidade tem intensidade igual a g. A intensidade da força tensora na corda, suposta ideal, vale:

a) 0,875 mg
b) 0,67 mg
c) 0,96 mg
d) 0,76 mg
e) 0,88 mg

LEITURA-RELACIONADA=3921 "Leis de Newton - Exercícios"]

Pratique mais Exercício sobre força de atrito.

Veja Terceira Lei de Newton.

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.