Exercícios sobre a área de figuras semelhantes (com respostas explicadas)
As figuras semelhantes são muito utilizadas em problemas de Geometria, pois mantêm a mesma forma, variando apenas de tamanho.
Confira exercícios resolvidos sobre área de figuras semelhantes, ideais para praticar a aplicação das razões de semelhança entre lados e áreas. Cada questão vem com resposta explicada passo a passo, ajudando a compreender melhor os conceitos e fortalecer o aprendizado em Matemática.
Questão 1
As áreas de dois polígonos regulares medem, respectivamente, e
. Sabendo que o lado do maior polígono mede
e que eles são semelhantes, qual deve ser o lado do polígono menor?
a)
b)
c)
d)
A razão de semelhança entre as áreas do menor e maior polígono é dada por:
Aplicando a razão de semelhança para os lados dos polígonos obtemos:
Questão 2
Uma fotografia de de área é ampliada de forma que suas dimensões aumentam em 150%. A área da fotografia ampliada, em
, será:
a) 20
b) 30
c) 40
d) 50
Podemos resolver a questão da seguinte forma:
Como não sabemos as dimensões da figura menor podemos supor que um de seus lados seja , portanto, com um aumento de 150% a figura ampliada terá como lado correspondente
.
Questão 3
Em um processo de desapropriação para ampliação de uma rodovia, a prefeitura utilizou uma planta topográfica em escala .
Um dos terrenos que será desapropriado ocupa uma área de na planta. Sabe-se que a indenização será paga com base no valor de R$ 200,00 por metro quadrado da área real.
O valor total a ser pago ao proprietário, em reais, será de:
a) R$ 200.000,00
b) R$ 2.000.000,00
c) R$ 20.000.000,00
d) R$ 200.000.000,00
Sabemos que escalas cartográficas são a razão de semelhança entre desenho e real na mesma unidade de medida, em nosso caso centímetros.
Como o valor da indenização é de R$ 200,00 por teremos:
Questão 4
Um artista cria uma tesselação no estilo de Escher usando um motivo animal e sua versão ampliada. Na tesselação, a figura ampliada cobre uma área de e a figura menor cobre
. Sabe-se que a altura da figura ampliada mede
.
Qual deve ser, em centímetros, a medida correspondente à altura da figura menor?
a) 3
b) 4
c) 5
d) 6
Sabemos que a razão de semelhança para áreas é igual ao quadrado da razão de semelhança para lementos lineares como base, altura, largura, comprimento, etc.
Questão 5
Dois triângulos e
são semelhantes. Os lados do triângulo
medem
,
e
. O perímetro do triângulo
é
. O valor da área do triângulo
, em
, é:
a)
b)
c)
d)
A razão de semelhança entre os triângulos ABC e DEF é:
Agora vamos calcular a área do triângulo ABC aplicando a Fórmula de Heron.
Para calcularmos a área do triângulo DEF usamos a razão de semelhança ao quadrado.
Questão 6
Observe a figura abaixo:
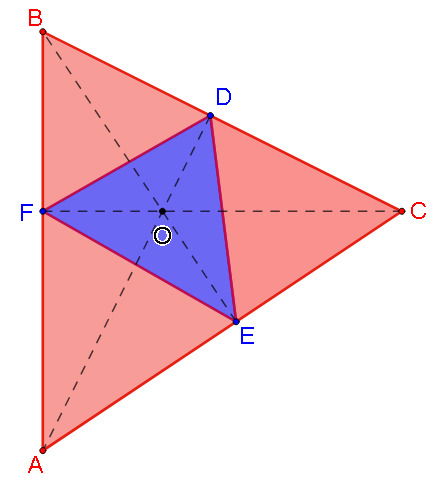
Sabendo que ,
,
e
é o ortocentro do triângulo
. A razão entre as áreas dos triângulos CDE e AFE vale:
a)
b)
c)
d)
Como CF é altura temos dois triângulos retângulos BFC e AFC nos quais podemos aplicar o Teorema de Pitágoras.
Pela semelhança, temos que AF e CD são os lados correspondentes nos triângulos AFE e CDE.
Utilizando a relação métrica em um triângulo qualquer temos:
Como temos CD e AF:
Questão 7
Um museu está projetando duas salas com formato elíptico: a sala principal e uma sala do sussurro. A sala principal tem semi-eixos medindo e
. A sala do sussurro deve ser semelhante à sala principal e ter área igual a
da área da sala principal. Quais são, respectivamente, os eixos maior e menor da sala do sussurro, em metros?
a) e
b) e
c) e
d) e
Para saber os valores dos eixos da elipse que corresponde a sala do sussuro podemos fazer:
Questão 8
Um resort está construindo duas piscinas retangulares: uma piscina principal e uma piscina infantil. A piscina principal mede 25 m de comprimento e 16 m de largura.
A piscina infantil deve ser semelhante à piscina principal e ter área igual a 1/4 da área da piscina principal. Qual a área da piscina infantil?
a)
b)
c)
d)
A área da piscina principal é dado pelo produto:
Como já temos a razão entre as áreas basta substituir as informações:
Continue praticando com exercícios sobre semelhança de polígonos (com gabarito).
Referências Bibliográficas
DANTE, Osvaldo. Matemática: Contexto & Aplicações. 2. ed. São Paulo: Ática, 2010.
MORGADO, Augusto César; WAGNER, Eduardo; JORGE, Miguel. Geometria I. Rio de Janeiro: Sociedade Brasileira de Matemática, 1990.
MORGADO, Augusto César; WAGNER, Eduardo; JORGE, Miguel. Geometria II. Rio de Janeiro: Sociedade Brasileira de Matemática, 1990.
CANELLAS, William. Exercícios sobre a área de figuras semelhantes (com respostas explicadas). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/exercicios-sobre-a-area-de-figuras-semelhantes-com-respostas-explicadas/. Acesso em:


