Exercícios sobre projeção ortogonal (com gabarito respondido)
Projeção ortogonal é a “sombra” de um ponto ou figura sobre um plano, ou reta, obtida traçando-se uma perpendicular do ponto até esse plano ou reta. Este é um tema recorrente no Enem.
Questão 1
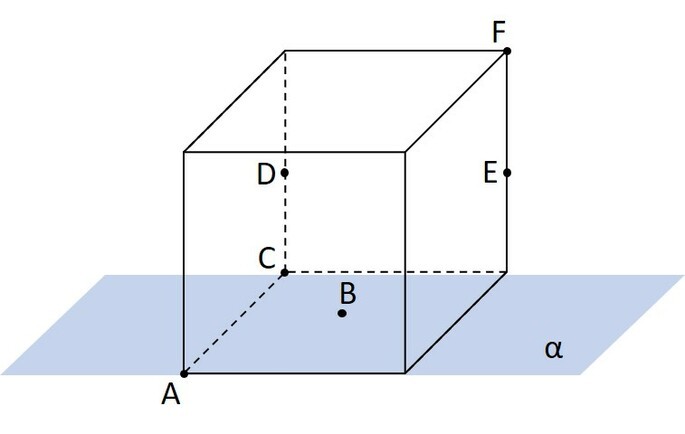
Considere o cubo da imagem abaixo apoiado em um plano α, e os pontos A – B – C – D – E – F. A projeção ortogonal destes pontos, nesta ordem, sobre o plano α é:
a) 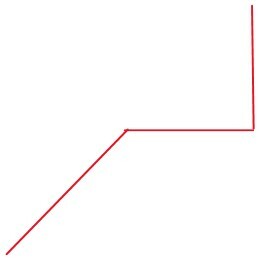
b) 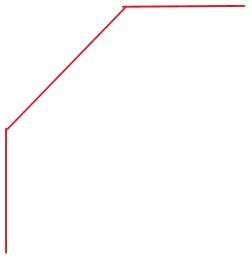
c) 
d) 
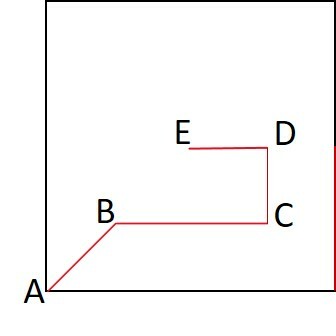
Ao ligar os pontos A, B e C, a linha poligonal formada já pertence ao plano α. A projeção ortogonal do segmento CD é o próprio ponto C.
A projeção ortogonal do segmento DE acompanha a aresta da base e a projeção do segmento EF é somente o ponto final da linha poligonal.
Questão 2
Uma lata na forma de um cilindro reto foi decorada com uma lista na cor laranja, da seguinte forma:
- A partir de um ponto da circunferência da base, uma linha vertical sobe 5 cm;
- No sentido anti-horário, uma linha paralela à base risca 1/3 da lateral;
- Na vertical para cima, um seguimento de reta de 5 cm;
- No sentido horário, uma linha paralela à base risca 1/2 da lateral;
- Na vertical para cima, um seguimento de reta de 5 cm até atingir a circunferência do topo da lata.
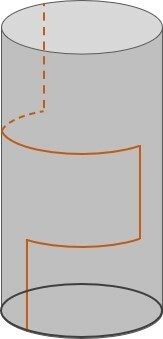
A projeção ortogonal da linha laranja sobre o plano do fundo da lata é:
a) 
b) 
c) 
d) 
A projeção ortogonal dos segmentos verticais são somente pontos sobre a base. A semicircunferência (1/2) se sobrepõe ao terço de circunferência.
Assim, a projeção ortogonal da linha laranja sobre o plano da base é a opção que descreve metade da circunferência.
Questão 3
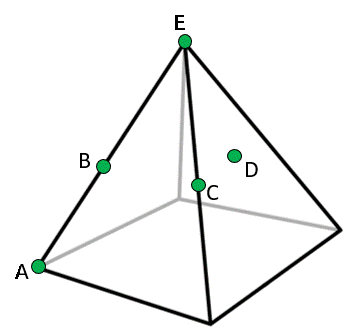
Considere a pirâmide de base quadrada da imagem. Após ligar os pontos A, B, C, D e E, nesta ordem e utilizando seguimentos de reta, a projeção ortogonal destes segmentos na base da pirâmide será:
a) 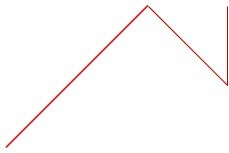
b) 
c) 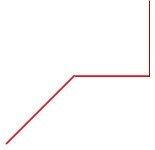
d) 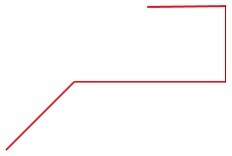
A projeção ortogonal da linha poligonal formada ao ligar os pontos por segmentos de reta é uma linha plana sobre a base.
Você pode imaginar a pirâmide sendo de vidro transparente, com o Sol posicionado ortogonalmente à pirâmide. A linha que procuramos é a sombra formada pelo ligação dos pontos.
Acompanhe melhor a linha sobre o plano da base com os pontos:
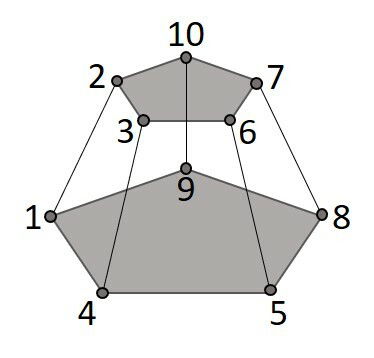
Questão 4
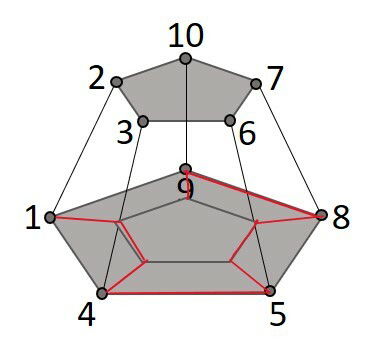
Após ligar os pontos de 1 ao 10, em ordem crescente e utilizando somente segmentos de reta, qual das seguintes opções representa a projeção ortogonal destes segmentos?
a) 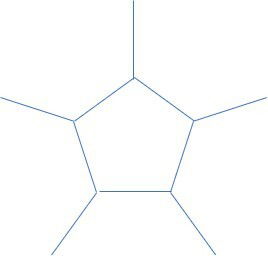
b) 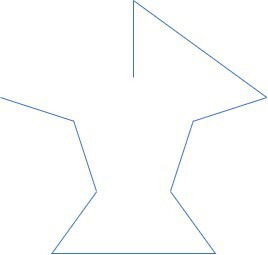
c) 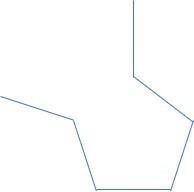
d) 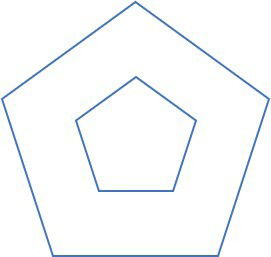
Para facilitar a visualização da projeção, acompanhe a marcação direto sobre o pentágono da base.
Questão 5
Duas ligações foram feitas sobre a superfície curva de um semicilindro: de A para B e de B para C. A projeção ortogonal destas ligações sobre o plano retangular será:
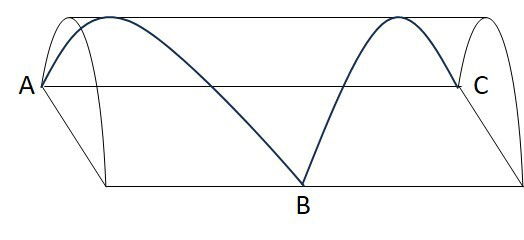
a) 
b) 
c) 
d) 
Embora as linhas façam curvas sobre a superfície cilíndrica, suas projeção são segmentos de reta sobre o retângulo da base.
As linhas não se cruzam, indo de A, até a metade do lado paralelo em B. Após, outro segmento liga o ponto B ao C.
Questão 6
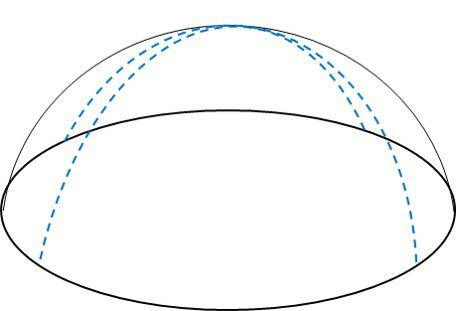
As projeções ortogonais das linhas curvas na semiesfera determinam a seguinte imagem no plano circular da base:
a) 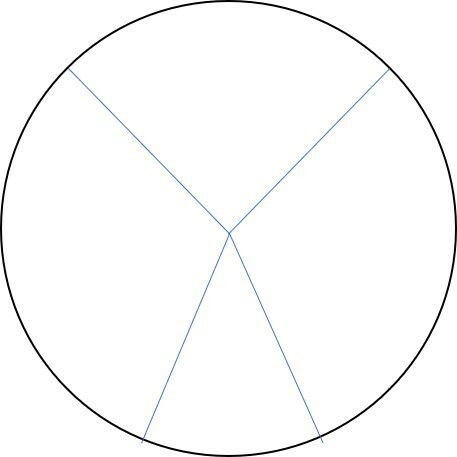
b) 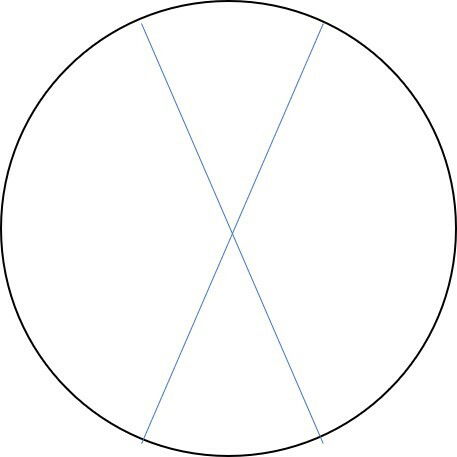
c) 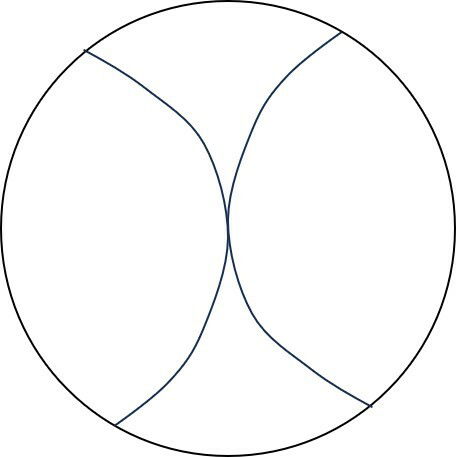
d) 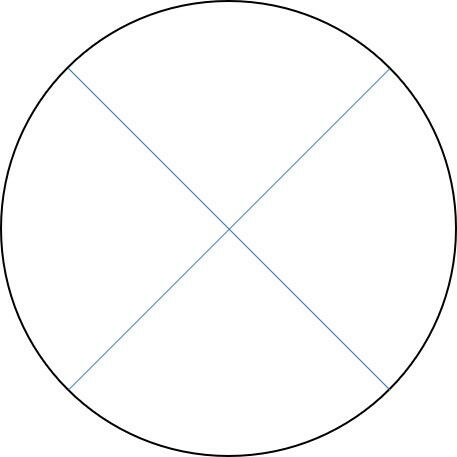
As linhas pontilhadas curvas sobre a semiesfera se cruzam perpendicularmente no círculo da base:
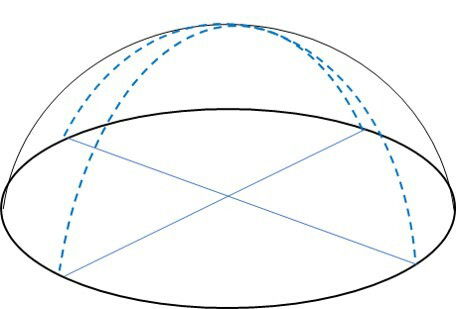
Veja também:
- Geometria Analítica: principais conceitos e fórmulas
- Projeções Cartográficas: O que são, tipos e exercícios
- Geometria espacial: quais são as figuras e suas fórmulas
- Geometria Plana
- Exercícios de geometria plana (com questões resolvidas)
- Exercícios de Geometria Espacial (com questões resolvidas)
ASTH, Rafael. Exercícios sobre projeção ortogonal (com gabarito respondido). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/exercicios-sobre-projecao-ortogonal/. Acesso em:


