Exercícios sobre quadriláteros com respostas explicadas
Estude sobre quadriláteros com esta lista de exercícios que preparamos para você. Tire suas dúvidas com as respostas explicadas passo a passo.
Questão 1
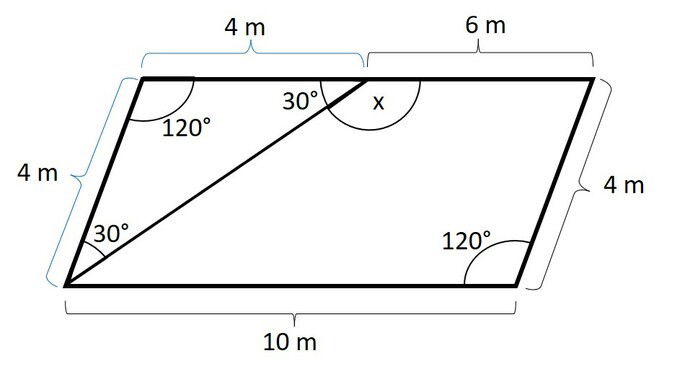
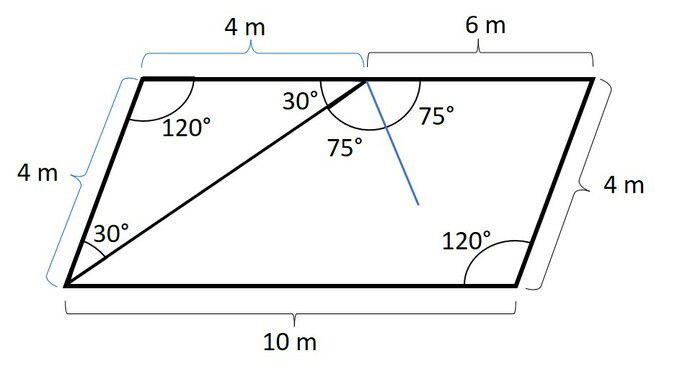
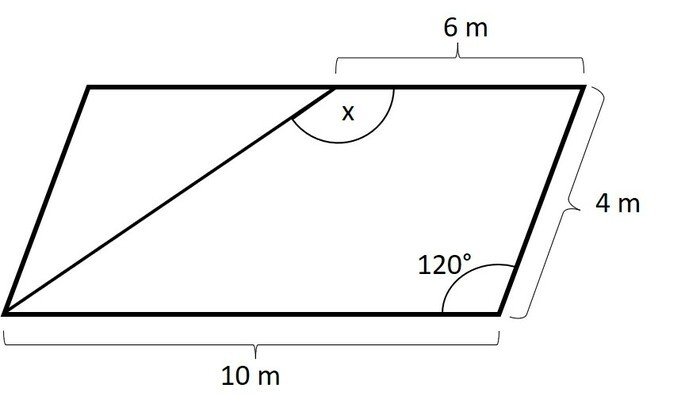
O quadrilátero abaixo é um paralelogramo. Determine o ângulo formado entre a bissetriz do ângulo x e o segmento de 6 m.
Questão 2
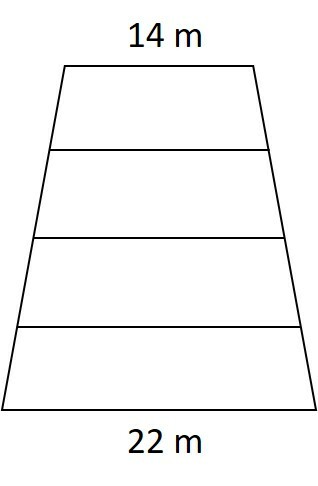
Na figura abaixo, as linhas horizontais são paralelas e equidistantes entre si. Determine a soma das medidas dos segmentos horizontais.
Questão 3
Determine os valores de x, y e w no trapézio isósceles abaixo.
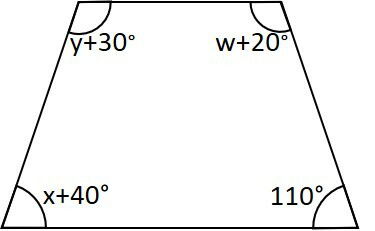
Questão 4
Considere o quadrilátero ABCD com os seguintes dados:
AB=8 cm, BC=10 cm, CD=8 cm, DA=10 cm
Avalie as seguintes afirmações e escolha a sequência correta:
- A diagonal BD é igual a diagonal AC.
- ABCD é um trapézio isósceles.
- ABCD é um losango.
- A soma dos ângulos internos de ABCD é 360∘.
a) Certo, Certo, Errado, Errado
b) Errado, Certo, Errado, Certo
c) Certo, Errado, Certo, Errado
d) Certo, Certo, Certo, Errado
e) Errado, Errado, Errado, Certo
1. A diagonal BD é maior que a diagonal AC. ERRADO.
O quadrilátero possui dois pares de lados com mesma medida, sendo um retângulo. Assim, suas diagonais possuem mesma medida.
2. ABCD é um trapézio isósceles. ERRADO.
Um trapézio possui apenas um par de lados opostos paralelos. Como AB=CD e BC=DA, temos dois pares de lados paralelos.
3. ABCD é um losango. ERRADO.
Um losango deve possuir todos os lados iguais.
4. A soma dos ângulos internos de ABCD é 360∘. CERTO.
A soma dos ângulos internos de todos os quadriláteros é igual a 360º.
Questão 5
Um quadrado com 64 cm² de área deve ser substituído por um trapézio retângulo de mesma área. Sabe-se que sua base maior possui 24 cm e sua altura, 4 cm. Qual deve ser a medida da base menor para possuir a mesma área do quadrado?
a) 4 cm
b) 6 cm
c) 8 cm
d) 10 cm
c) 12 cm
A área de um trapézio pode ser obtida por:
Onde:
- B é a base maior;
- b é a base menor;
- h é a altura;
- A é a área.
Substituindo os valores na fórmula e resolvendo para b:
Questão 6
(MACKENZIE)
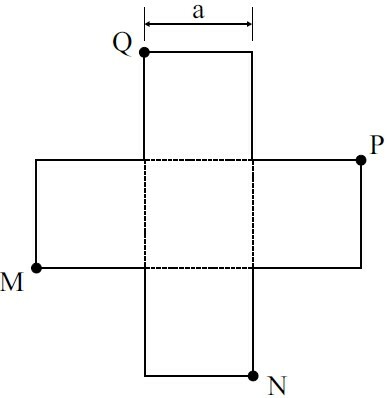
A figura acima é formada por quadrados de lados a.
A área do quadrilátero convexo de vértices M, N, P e Q é
a)
b)
c)
d)
e)
Como a figura é formada por quadrados, podemos determinar seguinte triângulo:
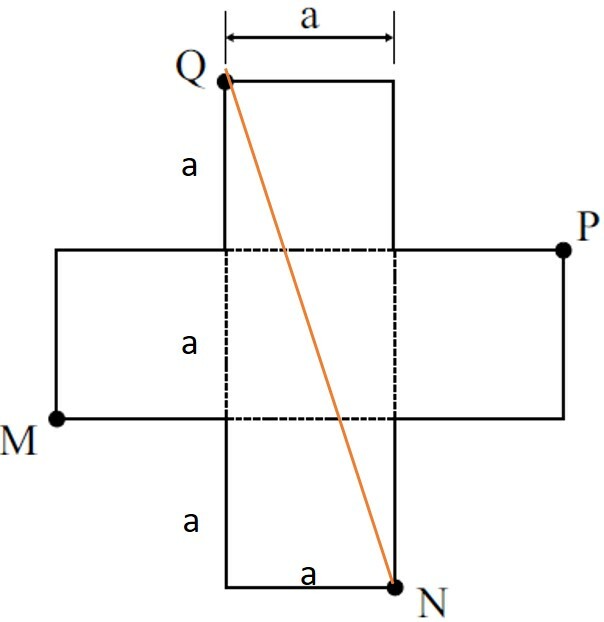
Assim, a diagonal do quadrado MNPQ é igual à hipotenusa do triângulo retângulo com altura 3a e base a.
Usando o Teorema de Pitágoras:
A medida de QN também é a hipotenusa do quadrado MNPQ. Utilizando mais uma vez o Teorema de Pitágoras e nomeando o lado do quadrado de l, temos:
Substituindo o valor de QN² obtido anteriormente:
Como a área do quadrado é obtida por l², é a medida da área do quadrado MNPQ.
Questão 7
(Enem 2017) Um fabricante recomenda que, para cada m2 do ambiente a ser climatizado, são necessários 800 BTUh, desde que haja até duas pessoas no ambiente. A esse número devem ser acrescentados 600 BTUh para cada pessoa a mais, e também para cada aparelho eletrônico emissor de calor no ambiente. A seguir encontram-se as cinco opções de aparelhos desse fabricante e suas respectivas capacidades térmicas:
Tipo I: 10 500 BTUh
Tipo II: 11 000 BTUh
Tipo III: 11 500 BTUh
Tipo IV: 12 000 BTUh
Tipo V: 12 500 BTUh
O supervisor de um laboratório precisa comprar um aparelho para climatizar o ambiente. Nele ficarão duas pessoas mais uma centrífuga que emite calor. O laboratório tem forma de trapézio retângulo, com as medidas apresentadas na figura.
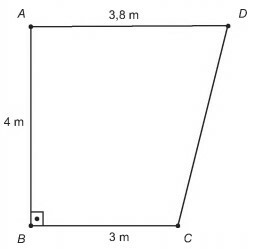
Para economizar energia, o supervisor deverá escolher o aparelho de menor capacidade térmica que atenda às necessidades do laboratório e às recomendações do fabricante.
A escolha do supervisor recairá sobre o aparelho do tipo
a) I.
b) II.
c) III.
d) IV.
e) V.
Começamos calculando a área do trapézio.
Multiplicando por 800 BTUh
13,6 x 800 = 10 880
Como além das duas pessoas também estará um aparelho que emite calor, conforme o fabricante, devemos acrescentar 600 BTUh.
10 880 + 600 = 11480 BTUh
Logo, o supervisor deve escolher o número III.
Questão 8
(Enem 2009) O governo cedeu terrenos para que famílias construíssem suas residências com a condição de que no mínimo 94% da área do terreno fosse mantida como área de preservação ambiental. Ao receber o terreno retangular ABCD, em que AB= BC/2 , Antônio demarcou uma área quadrada no vértice A, para a construção de sua residência, de acordo com o desenho, no qual AE = AB/5 é lado do quadrado.
Nesse caso, a área definida por Antônio atingiria exatamente o limite determinado pela condição se ele
a) duplicasse a medida do lado do quadrado.
b) triplicasse a medida do lado do quadrado.
c) triplicasse a área do quadrado.
d) ampliasse a medida do lado do quadrado em 4%.
e) ampliasse a área do quadrado em 4%.
Nomearemos o segmento da área para construção de x.
AE = x
Como conforme enunciado, AE = AB/5, logo:
Ainda, como AB = BC/2:
A área construída é .
A área total é .
Se , então:
Como o limite de área construída é de 6%, ele pode triplicar a área.
3 . 2% = 6%
Questão 9
(UECE) Os pontos M, N, O e P são os pontos médios dos lados XY, YW, WZ e ZX do quadrado XYWZ. Os segmentos YP e ZM cortam-se no ponto U e os segmentos OY e ZN cortam-se no ponto V. Se a medida do lado do quadrado XYWZ é 12 m então a medida, em m2 , da área do quadrilátero ZUYV é
a) 36.
b) 60.
c) 48.
d) 72.
A situação descrita no enunciado é:
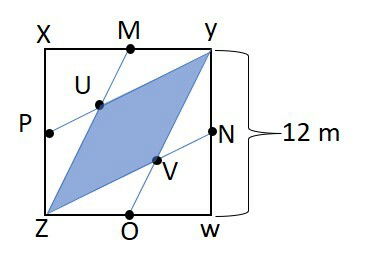
A figura formada é um losango e sua área pode ser determinada como:
A diagonal maior do losango também é a diagonal do quadrado que pode ser determinada pelo teorema de Pitágoras.
A diagonal menor é um terço da diagonal maior. Substituindo na fórmula da área, temos:
Aprenda mais em:
- Quadriláteros: o que são, tipos, exemplos, área e perímetro
- O que é um Paralelogramo?
- Trapézio
- Áreas de Figuras Planas
- Área de Figuras Planas: Exercícios Resolvidos e Comentados
ASTH, Rafael. Exercícios sobre quadriláteros com respostas explicadas. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/exercicios-sobre-quadrilateros/. Acesso em: