Exercícios sobre velocidade vetorial média (com questões resolvidas e explicadas)
A velocidade vetorial média é uma grandeza vetorial que se diferencia da velocidade escalar média por considerar não somente o módulo (valor numérico), mas também a direção e o sentido do movimento.
Aplique seus conhecimentos sobre cinemática vetorial nas questões a seguir e esclareça suas dúvidas com as resoluções detalhadas!
Questão 1
Durante uma operação de resgate em área urbana, um drone da Defesa Civil precisa sair de sua base localizada no ponto A, realizar uma missão de reconhecimento no ponto B e retornar à base. Para otimizar o tempo de operação, o piloto programa o drone para seguir uma trajetória específica.
O drone parte do ponto A, voa 600 m para o norte até o ponto B, onde permanece por 2 minutos coletando dados. Em seguida, voa 800 m para o leste até o ponto C, onde encerra a missão após 1 minuto de transmissão das informações coletadas. Todo o voo (sem contar as paradas) dura 5 minutos.
Considerando que o sistema de coordenadas tem origem na base A, com o eixo x apontando para o leste e o eixo y para o norte, qual é o módulo da velocidade vetorial média do drone durante todo o período da operação (incluindo as paradas)?
a) 87,5 m/min
b) 100 m/min
c) 125 m/min
d) 175 m/min
e) 200 m/min
Dados do problema:
- Trajeto AB: 600 m para o norte
- Tempo de parada em B: 2 min
- Trajeto BC: 800 m para o leste
- Tempo de parada em C: 1 min
- Tempo total de voo: 5 min
- Tempo total da operação: 5 + 2 + 1 = 8 min
Passo 1: Estabelecer o sistema de coordenadas.
Base A: origem (0, 0)
Ponto B: (0, 600) — 600 m ao norte
Ponto C: (800, 600) — 800 m ao leste de B
Passo 2: Calcular o deslocamento vetorial total.
O conceito fundamental aqui é que a velocidade vetorial média depende somente do deslocamento vetorial (vetor que liga a posição inicial à posição final) e do tempo total.
O drone vai da base A até o ponto C:
Posição inicial: A (0, 0)
Posição final: C (800, 600)
Deslocamento vetorial = Posição final - Posição inicial = (800, 600) - (0, 0) = (800, 600)
O módulo do deslocamento vetorial é:
Passo 3: Aplicar a definição de velocidade vetorial média.
A velocidade vetorial média é definida como:
Onde:
-
= deslocamento vetorial - Δt = intervalo de tempo total
Passo 4: Calcular o resultado.
O módulo da velocidade vetorial média é:
Resposta correta: c) 125 m/min
Questão 2
Em uma operação de emergência médica, um helicóptero do SAMU precisa resgatar um paciente em estado grave no topo de um edifício. O helicóptero parte da base hospitalar localizada ao nível do mar, sobe verticalmente até uma altura de 120 metros onde se encontra a plataforma de pouso do edifício, permanece 3 minutos para o embarque do paciente, e retorna verticalmente até a base hospitalar.
Durante todo o voo de subida, o helicóptero mantém velocidade constante, levando 2 minutos para atingir a altura máxima. Na descida, por questões de segurança com o paciente a bordo, o piloto reduz a velocidade e leva 3 minutos para retornar ao solo.
Considerando o sistema de coordenadas com origem na base hospitalar e eixo vertical apontando para cima, qual é o módulo da velocidade vetorial média do helicóptero durante toda a operação de resgate (incluindo o tempo de embarque)?
a) 60 m/min
b) 30 m/min
c) 15 m/min
d) 7,5 m/min
e) zero
Dados do problema:
- Altura do edifício: 120 m
- Tempo de subida: 2 min
- Tempo de embarque no topo: 3 min
- Tempo de descida: 3 min
- Tempo total da operação: 2 + 3 + 3 = 8 min
Passo 1: Estabelecer o sistema de coordenadas.
Base hospitalar: origem (0 m) — posição inicial
Topo do edifício: altura +120 m
Retorno à base: origem (0 m) — posição final
Passo 2: Analisar o movimento.
O helicóptero realiza um movimento vertical com três fases:
- Subida: de 0 m até +120 m;
- Permanência: mantém-se em +120 m;
- Descida: de +120 m até 0 m.
Passo 3: Calcular o deslocamento vetorial total.
A velocidade vetorial média depende somente do deslocamento vetorial (diferença entre posição final e inicial) e do tempo total.
- Posição inicial: 0 m (base hospitalar)
- Posição final: 0 m (base hospitalar)
Deslocamento vetorial = Posição final - Posição inicial = 0 - 0 = 0 m
Passo 4: Conclusão.
Quando um objeto retorna à sua posição inicial, sua velocidade vetorial média é sempre zero, independentemente de:
- A distância total percorrida (240 m neste caso);
- A velocidade em cada trecho do movimento;
- O tempo gasto em cada fase da operação;
- A complexidade da trajetória.
Resposta correta: e) zero
Diferença conceitual importante:
Velocidade escalar média: distância total ÷ tempo total = 240 m ÷ 8 min = 30 m/min
Velocidade vetorial média: deslocamento vetorial ÷ tempo total = 0 m ÷ 8 min = 0 m/min
Questão 3
Durante uma operação de monitoramento ambiental, um barco científico navega em águas calmas para coletar amostras de água em diferentes pontos de um lago. O sistema de GPS do barco registra que ele mantém uma velocidade vetorial constante de módulo 10 m/s durante toda a operação.
Os dados coletados pelo GPS mostram que o barco percorre uma trajetória específica para otimizar a coleta de amostras, sempre mantendo a mesma velocidade vetorial, durante todo o percurso.
Com base nos princípios da cinemática vetorial, qual das seguintes afirmações descreve corretamente a trajetória do barco durante esta operação?
a) A trajetória é necessariamente uma circunferência, pois o módulo da velocidade é constante.
b) A trajetória pode ser curvilínea qualquer, desde que o barco mantenha o módulo da velocidade constante.
c) A trajetória deve ser obrigatoriamente retilínea, pois a velocidade vetorial é constante.
d) A trajetória é uma parábola, pois o movimento é uniforme.
e) A trajetória pode ser retilínea ou curvilínea, dependendo das condições ambientais.
Conceito fundamental da questão: Velocidade vetorial constante.
Para compreender esta questão, é essencial distinguir entre:
- Velocidade escalar constante: somente o módulo (valor numérico) da velocidade permanece constante;
- Velocidade vetorial constante: módulo, direção e sentido permanecem constantes.
Análise das condições do problema:
O enunciado especifica que o barco mantém velocidade vetorial constante, o que significa:
- Módulo constante: 10 m/s;
- Direção constante: mesma direção durante todo o percurso;
- Sentido constante: mesmo sentido durante todo o percurso.
Implicações físicas da velocidade vetorial constante:
Quando a velocidade vetorial é constante o vetor velocidade não muda, isso significa que:
Não há aceleração;
Movimento retilíneo uniforme: Um corpo só pode manter velocidade vetorial constante se seguir uma trajetória retilínea;
Impossibilidade de trajetória curva: Qualquer mudança na direção do movimento (trajetória curva) exigiria aceleração centrípeta, contradizendo a velocidade vetorial constante.
Análise das alternativas
a) Incorreta: Uma circunferência exige mudança constante na direção da velocidade (aceleração centrípeta).
b) Incorreta: Qualquer trajetória curvilínea implica mudança na direção da velocidade.
c) CORRETA: Velocidade vetorial constante só é possível em movimento retilíneo uniforme.
d) Incorreta: Movimento parabólico envolve aceleração gravitacional.
e) Incorreta: Trajetória curvilínea é incompatível com velocidade vetorial constante.
Resposta correta: c) A trajetória deve ser obrigatoriamente retilínea, pois a velocidade vetorial é constante.
Questão 4
Durante uma operação de entrega de medicamentos em uma região de emergência sanitária, um drone autônomo precisa navegar por uma área urbana organizada em quarteirões quadrados regulares. O sistema de controle do drone foi programado para seguir as ruas, que são paralelas entre si e distam 80 metros uma da outra.
O drone parte do ponto P (centro de distribuição médica) e deve chegar ao ponto Q (posto de saúde).
A trajetória programada faz o drone seguir pelas ruas:
- 4 quarteirões para o leste;
- 2 quarteirões para o sul.
Durante todo o percurso, o drone mantém velocidade escalar constante de 16 m/s. Ao chegar no ponto Q, o drone permanece 45 segundos para a entrega dos medicamentos, encerrando a operação neste local.
Considerando somente o trajeto de P até Q (incluindo o tempo de entrega), o módulo da velocidade vetorial média do drone durante esta operação é mais próxima de
a) 2,4 m/s.
b) 4,8 m/s.
c) 6,4 m/s.
d) 8,0 m/s.
e) 10,7 m/s.
Dados do problema:
- Distância entre ruas paralelas: 80 m
- Trajetória: 4 quarteirões leste + 2 quarteirões sul
- Velocidade escalar constante durante o voo: 16 m/s
- Tempo de entrega no ponto Q: 45 s
Passo 1: Estabelecer o sistema de coordenadas.
Considerando P como origem (0, 0):
- 4 quarteirões leste: 4 × 80 = 320 m
- 2 quarteirões sul: 2 × 80 = 160 m (coordenada negativa)
- Ponto P (posição inicial): (0, 0)
- Ponto Q (posição final): (320, -160)
Passo 2: Calcular o deslocamento vetorial.
O deslocamento vetorial é o vetor que liga diretamente a posição inicial à posição final. Este vetor deslocamento forma com os catetos 320 e -160 um triângulo retângulo.
= Posição final - Posição inicial = (320, -160) - (0, 0) = (320, -160)
O módulo do deslocamento vetorial é:
Passo 3: Calcular o tempo total da operação.
Tempo de voo (P → Q pelas ruas):
Distância percorrida: 4 × 80 + 2 × 80 = 320 + 160 = 480 m
Tempo: 480 m ÷ 16 m/s = 30 s
Tempo de entrega: 45 s
Tempo total: 30 + 45 = 75 s
Passo 4: Aplicar a definição de velocidade vetorial média
A velocidade vetorial média é definida como:
Calculando o módulo:
Resposta correta: b) 4,8 m/s
Questão 5
Durante uma enchente em uma região metropolitana, uma equipe de resgate utiliza um barco anfíbio para evacuar famílias ilhadas. O barco parte da base de operações localizada na margem norte de um rio e precisa atravessar até uma comunidade na margem sul, onde permanecem pessoas em situação de risco.
Devido à forte correnteza do rio, o piloto programa uma rota específica: o barco navega 800 metros em direção ao leste (paralelo à margem norte) e, em seguida, 600 metros em direção ao sul para atravessar o rio perpendicularmente. Durante todo o trajeto, o barco mantém velocidade escalar constante de 20 m/s.
Ao chegar à comunidade, a equipe realiza o resgate durante 4 minutos. Devido ao agravamento das condições meteorológicas, o comando decide que o barco deve permanecer na comunidade para dar suporte às operações locais, encerrando sua missão neste local.
Considerando o sistema de coordenadas com origem na base de operações, eixo x apontando para o leste e eixo y para o sul, qual é o módulo da velocidade vetorial média do barco durante toda a operação (trajeto mais tempo de resgate)?
a) 2,0 m/s
b) 3,2 m/s
c) 4,5 m/s
d) 6,4 m/s
e) 10,0 m/s
Dados do problema:
- Trajeto: 800 m leste + 600 m sul (sem volta)
- Velocidade escalar constante: 20 m/s
- Tempo de resgate: 4 min = 240 s
Passo 1: Estabelecer as posições.
Sistema de coordenadas com origem na base:
Base (posição inicial e final): (0, 0)
Comunidade (após trajeto em L): (800, 600)
Passo 2: Calcular o tempo total da operação.
Trajeto (base → comunidade):
Distância percorrida: 800 + 600 = 1400 m
Tempo: 1400 m ÷ 20 m/s = 70 s
Resgate na comunidade: 240 s
Tempo total: 70 + 240 = 310 s
Passo 3: Calcular o deslocamento vetorial.
O barco parte da base e encerra a operação na comunidade:
Posição inicial: (0, 0) — base de operações
Posição final: (800, 600) — comunidade
Deslocamento vetorial:
= (800, 600) - (0, 0) = (800, 600)
O módulo do deslocamento vetorial é:
Passo 4: Aplicar a definição de velocidade vetorial média.
Conceito-chave: deslocamento vetorial em linha reta.
Resposta correta: b) 3,2 m/s
Questão 6
Um caminhoneiro efetuou duas entregas de mercadorias seguindo rigorosamente o itinerário indicado pelos vetores deslocamento d₁ e d₂ ilustrados na figura. Para a primeira entrega, ele deslocou-se 8 km em linha reta partindo do depósito. Para a segunda entrega, percorreu uma distância de 4 km em uma direção que forma 30° com a horizontal, conforme mostrado no diagrama.
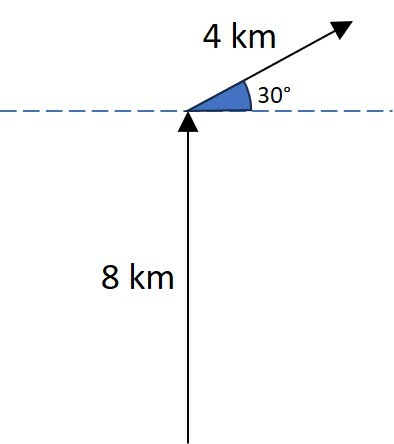
O tempo gasto na primeira entrega foi de 20 minutos e na segunda entrega foi de 15 minutos. Ao final da segunda entrega, a distância em linha reta que o caminhoneiro se encontra do ponto de partida e sua velocidade vetorial média durante todo o percurso são, respectivamente:
a) 14,0 km e 24,0 km/h
b) 13,0 km e 22,3 km/h
c) 12,0 km e 20,6 km/h
d) 11,0 km e 18,9 km/h
e) 10,6 km e 18,1 km/h
A velocidade vetorial média considera somente o deslocamento resultante (vetor que liga a posição inicial à posição final) dividido pelo tempo total, independentemente da trajetória seguida.
Dados do problema:
- Primeiro deslocamento: d₁ = 8 km (vertical, para cima)
- Segundo deslocamento: d₂ = 4 km (30° com a horizontal)
- Tempo primeira entrega: t₁ = 20 min = 1/3 h
- Tempo segunda entrega: t₂ = 15 min = 1/4 h
- Tempo total: Δt = 35 min = 7/12 h
Passo 1: Determinar as componentes do segundo deslocamento.
Para d₂ = 4 km a 30° da horizontal:
Componente horizontal: d₂ₓ = 4 × cos(30°) = 4 × (√3/2) = 2√3 km
Componente vertical: d₂ᵧ = 4 × sen(30°) = 4 × (1/2) = 2 km
Passo 2: Calcular a posição final.
Posição final em relação ao ponto de partida:
- Coordenada x: 0 + 2√3 = 2√3 km
- Coordenada y: 8 + 2 = 10 km
Para ordenado: (2√3, 10)
Passo 3: Calcular o deslocamento resultante
Usando o teorema de Pitágoras:
Passo 4: Calcular a velocidade vetorial média.
Resposta: alternativa e) 10,6 km e 18,1 km/h
Questão 7
Os satélites geoestacionários são fundamentais para as telecomunicações modernas, mantendo-se sempre na mesma posição relativa à superfície terrestre. Um satélite de comunicações orbita a Terra em uma trajetória circular a 35786 km de altitude, completando uma volta em 24 horas para acompanhar a rotação terrestre.
Um engenheiro de controle de missão precisa calcular a velocidade vetorial média do satélite entre dois pontos específicos de sua órbita. Considerando um referencial inercial fixo no espaço, o satélite percorre um arco correspondente a um ângulo central de 60° em exatamente 4 horas, desde um ponto de referência R até um ponto B.
Dados: Raio da Terra = 6370 km.
A velocidade vetorial média do satélite no trecho RB é aproximadamente:
a) 2 786 km/h
b) 3 156 km/h
c) 5 431 km/h
d) 6 262 km/h
e) 10 539 km/h
Dados do problema:
- Altitude do satélite: h = 35.786 km
- Raio da Terra: R_T = 6.370 km
- Ângulo central percorrido: θ = 60°
- Tempo para percorrer o arco: Δt = 4 h
- Período orbital: T = 24 h
Passo 1: Calcular o raio da órbita.
Raio da órbita = Raio da Terra + Altitude
Raio da órbita = 6.370 + 35.786
Raio da órbita = 42.156 km
Passo 2: Determinar o deslocamento vetorial.
Para um arco de 60° em uma trajetória circular, o deslocamento vetorial (corda RB) é exatamente a medida do lado de um triângulo equilátero.
Os seguimentos que formam o ângulo central são iguais, logo o triângulo é isósceles. Isto implica que os ângulos da base devem ser iguais.
Como a soma dos ângulos de um triângulo é sempre (180°) e já temos 60°:
180–60 = 120
Os 120° divididos para os ângulos da base (iguais) fornecem 60º para cada.
Logo, o triângulo é equilátero e o deslocamento RB é igual à medida do raio da órbita: 42 156 km.
Passo 3: Calcular a velocidade vetorial média.
Resposta: alternativa e) 10 539 km/h
Aprenda mais com:
- Exercícios sobre velocidade escalar média
- Grandezas Vetoriais
- Vetores: soma, subtração e decomposição
- Velocidade relativa: o que é, como calcular, exemplos
- Vetores: o que são, operações, aplicações e exercícios
- Cinemática: conceito e fórmulas
- Fórmulas de cinemática
ASTH, Rafael. Exercícios sobre velocidade vetorial média (com questões resolvidas e explicadas). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/exercicios-sobre-velocidade-vetorial-media/. Acesso em:
