🔥 Turbine seus estudos com 47% OFF
no Toda Matéria+

Turbine seus estudos com 47% OFF no Toda Matéria+

Tronco de cone: quais os principais elementos e como calcular (com exemplos)

Rafael C. Asth

Professor de Matemática e Física

O tronco de cone é um sólido geométrico formado pela parte do cone compreendida entre a base e um plano paralelo à base, que secciona este cone.

É uma forma geométrica muito presente no nosso dia a dia: baldes, vasos de plantas, copos descartáveis, luminárias e até algumas estruturas arquitetônicas têm esse formato.

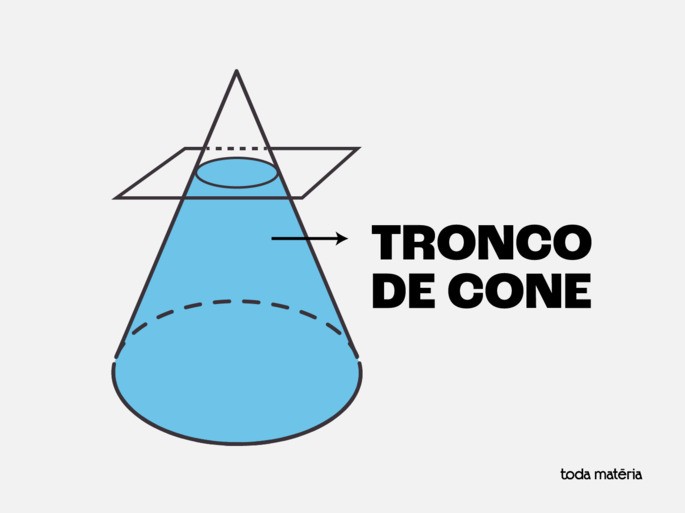
Tronco de cone exemplo.

Elementos do tronco de cone

Para trabalhar com tronco de cone, precisamos conhecer seus elementos principais:

Base maior (R): É a base original do cone, com raio maior.
Base menor (r): É a base formada pelo corte paralelo, com raio menor.
Altura (h): Distância perpendicular entre as duas bases paralelas.
Geratriz (g): Segmento de reta que une um ponto da circunferência da base maior a um ponto correspondente da circunferência da base menor.
Eixo: Reta que passa pelos centros das duas bases.

Remover anúncios

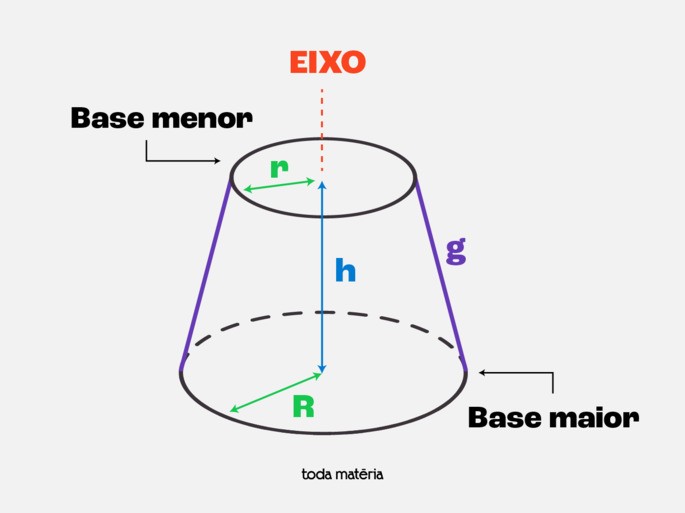
Observação importante: Num tronco de cone reto (o mais comum), o eixo é perpendicular às bases e a geratriz forma uma superfície lateral inclinada.

Relação entre os elementos:

Pelo Teorema de Pitágoras aplicado ao tronco de cone, temos:

$g ao quadrado igual a h ao quadrado mais parêntese esquerdo R menos r parêntese direito ao quadrado$

Área da Base Maior (AB)

As bases de um tronco de cone são círculos. Para determinar a área da base maior, utilizamos o raio (R) da base maior.

$A B igual a pi R ao quadrado$

Área da Base Menor (Ab)

Utilizando o raio menor.

Remover anúncios

$A B igual a pi r ao quadrado$

Área Lateral (AL)

A área lateral corresponde à superfície inclinada que conecta ambas as bases:

$A L igual a pi g parêntese esquerdo R mais r parêntese direito$

Exemplo: Calculando a área total de um tronco de cone.

Um tronco de cone possui raios de 9 cm e 4 cm, altura de 12 cm. Calcule sua área total. (Use π=3,14)

Resolução:

Passo 1: Calcular a geratriz.

$g ao quadrado igual a h ao quadrado mais parêntese esquerdo R menos r parêntese direito ao quadrado g ao quadrado igual a 12 ao quadrado mais parêntese esquerdo 9 menos 4 parêntese direito ao quadrado g ao quadrado igual a 144 mais 25 g ao quadrado igual a 169 g igual a raiz quadrada de 169 g igual a 13 espaço c m$

Passo 2: Calcular a área total.

A área total é a soma das áreas das bases mais a lateral.

Área da base menor:

$A B igual a pi r ao quadrado A B igual a pi 4 ao quadrado A B igual a 16 pi$

Área da base maior:

$A B igual a pi R ao quadrado A B igual a pi 9 ao quadrado A B igual a 81 pi$

Área lateral:

$A L igual a pi parêntese esquerdo R mais r parêntese direito vezes g A L igual a pi parêntese esquerdo 9 mais 4 parêntese direito vezes 13 A L igual a pi 13 espaço vezes 13 A L igual a 169 pi$

Somando as parcelas:

$Á r e a espaço t o t a l igual a 16 pi espaço mais espaço 81 pi espaço mais espaço 169 pi Á r e a espaço t o t a l igual a 266 pi espaço$

Substituindo o valor de $pi$ :

$Á r e a espaço t o t a l igual a 266 espaço. espaço 3 vírgula 14 espaço Á r e a espaço t o t a l igual a 835 vírgula 24 espaço c m ao quadrado$

Volume (V)

O volume do tronco de cone é calculado pela fórmula:

$V igual a h sobre 3 parêntese esquerdo A B mais A b mais raiz quadrada de A B espaço. espaço A b fim da raiz parêntese direito$

Uma alternativa é "abrir" as fórmulas das áreas das bases e colocar o $pi$ em evidência:

$V igual a numerador pi h sobre denominador 3 fim da fração parêntese esquerdo R ao quadrado mais R. r mais r ao quadrado parêntese direito$

Exemplo: Calculando o volume de um tronco de cone.

Um recipiente em forma de tronco de cone tem 12 cm de altura, raio da base maior igual a 9 cm e raio da base menor igual a 4 cm. Qual é a capacidade desse recipiente? (Use π=3,14)

Usando a fórmula do volume:

$V igual a numerador pi h sobre denominador 3 fim da fração parêntese esquerdo R ao quadrado mais R. r mais r ao quadrado parêntese direito V igual a numerador 3 vírgula 16 espaço. espaço 12 sobre denominador 3 fim da fração parêntese esquerdo 81 mais 9.4 mais 16 parêntese direito V igual a numerador 37 vírgula 92 sobre denominador 3 fim da fração parêntese esquerdo 81 mais 36 mais 16 parêntese direito V igual a numerador 37 vírgula 92 sobre denominador 3 fim da fração parêntese esquerdo 133 parêntese direito V igual a numerador 5.043 vírgula 36 sobre denominador 3 fim da fração V igual a 1.681 vírgula 12 espaço c m ao cubo$

Remover anúncios

Questões sobre tronco de cone

Questão 1

Um fabricante de baldes precisa calcular a quantidade de material necessário para produzir um balde em forma de tronco de cone. O balde tem raio da base maior de 20 cm, raio da base menor de 15 cm e altura de 30 cm. Qual é, aproximadamente, a medida da geratriz desse balde?

a) 25,5 cm

b) 30,4 cm

c) 31,4 cm

d) 35,2 cm

e) 40,0 cm

Questão 2

Um reservatório de água tem formato de tronco de cone com 2 m de altura, raio da base inferior de 3 m e raio da base superior de 1,5 m. Considerando π = 3, qual é a capacidade aproximada desse reservatório?

a) 18 m³

b) 21 m³

c) 24 m³

d) 27 m³

e) 31,5 m³

Remover anúncios

Questão 3

Uma indústria produz peças metálicas em forma de tronco de cone. Para calcular o custo de pintura, é necessário conhecer a área lateral de cada peça. Sabendo que uma peça tem raios de 12 cm e 8 cm, e geratriz de 10 cm, qual é sua área lateral? (Use π = 3,14)

a) 502,4 cm²

b) 628,0 cm²

c) 753,6 cm²

d) 879,2 cm²

e) 1.004,8 cm²

Veja também:

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.

Remover anúncios