Exercícios sobre operações com arcos (com questões explicadas)

Em um centro de distribuição, foi instalada uma rampa hidráulica ajustável para facilitar o carregamento de caminhões de diferentes alturas. A rampa possui um sistema automatizado que permite ao operador ajustar sua inclinação por um painel digital.

Inicialmente, a rampa está posicionada a 45° em relação à horizontal. Quando é necessário reduzir a inclinação para acomodar veículos mais baixos, o operador digita no painel o valor do ângulo θ (em graus) que deseja diminuir da inclinação inicial.

O mecanismo da rampa funciona de forma que o ponto de apoio da superfície se move verticalmente, alterando a altura h, mas mantendo sempre uma distância horizontal fixa L em relação ao ponto O de rotação da rampa.

A figura ilustra essa situação:

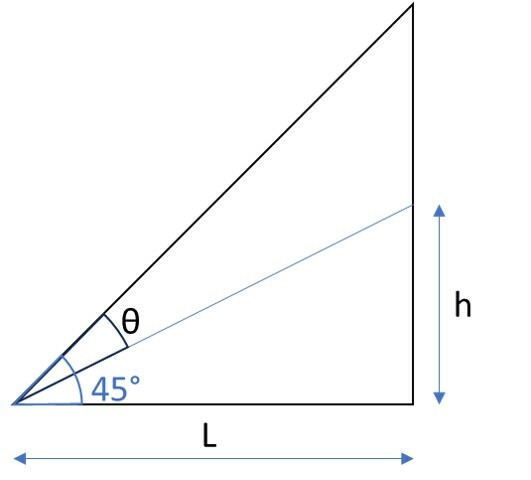
A expressão que permite calcular a altura h em função do ângulo θ é:

Em um condomínio residencial de alto padrão, foi instalado um moderno sistema de videomonitoramento com câmeras inteligentes que realizam varreduras automáticas programáveis. Uma dessas câmeras, posicionada no hall de entrada, executa um padrão de movimento específico para cobrir toda a área de interesse.

O sistema funciona da seguinte forma: a câmera realiza dois giros consecutivos programados no mesmo sentido. Primeiro, ela gira um arco de x graus, permanece parada por alguns segundos para estabilizar a imagem, e então gira mais um arco de y graus. Os valores dos arcos e o tempo das pausas são configuráveis pelo administrador do sistema por meio de um software de controle.

Após completar ambos os arcos em um sentido, a câmera automaticamente retorna à posição inicial, repetindo o mesmo movimento no sentido oposto, garantindo assim uma cobertura completa e uniforme da área monitorada, sendo (90º) a amplitude máxima de giro em cada sentido.

O software de controle caracteriza matematicamente todo o movimento através do cálculo do seno do ângulo total percorrido em um sentido. Há cinco configurações disponíveis ao usuário, representadas pelos números inteiros de 1 a 5. Estes valores são utilizados pelo software para determinar as medidas dos arcos de cada movimento.

Para otimizar o desempenho do sistema, o administrador costuma configurar ambos os arcos com valores iguais, escolhendo a opção

A prefeitura de uma cidade construiu um parque municipal com um grande lago circular de 150 metros de raio. Ao redor do lago foi planejada uma calçada para caminhadas e práticas esportivas, aproveitando toda a circunferência.

O projeto foi dividido em etapas, partindo da entrada principal (ponto A) e seguindo no sentido anti-horário:

O arco x (de medida π/3 radianos) vai da entrada A até o ponto B, onde foram instalados bancos para descanso e plantadas árvores para sombra;

Continuando, o arco y (de medida π/4 radianos) vai do ponto B até a saída C, próxima ao estacionamento;

Seguindo o percurso, o arco z (de medida π/6 radianos) vai da saída C até o ponto D, onde foi construída uma academia ao ar livre com aparelhos de ginástica.

A construção do calçamento já foi concluída até o ponto D. Para finalizar a obra, é necessário calcular quantos metros ainda faltam para completar todo o perímetro circular.

A quantidade mais próxima de metros de calçamento que ainda faltam para completar a circunferência do lago é de

Use π = 3,14.

Em um projeto de revitalização urbana, foi construída uma praça circular com 80 metros de diâmetro. No centro da praça (ponto O), será instalada uma fonte ornamental. O paisagista responsável precisa posicionar cinco pontos de iluminação LED (A, B, C, D e E).

Para criar um efeito visual harmonioso, o sistema de iluminação foi projetado de forma que:

Os pontos A, B, D e E estejam posicionados na circunferência da praça;

O ponto C esteja localizado no interior da praça, entre o centro O e a borda;

As luzes em A e B serão conectadas por um cabo subterrâneo;

As luzes em D e E também serão conectadas por outro cabo subterrâneo.

Durante os testes de instalação, o engenheiro elétrico mediu o ângulo ACB (formado pelas linhas que conectam C aos pontos A e B) e obteve 65°. Com base nessa medição ele precisa calcular o comprimento total dos cabos que conectarão os pares de luzes.

A figura, fora de escala e meramente ilustrativa, mostra a disposição dos pontos:

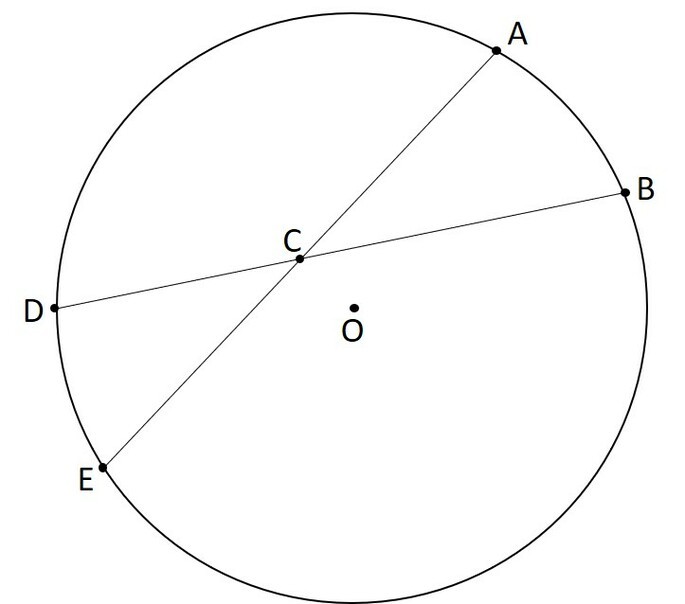
Considerando que AB e DE são arcos, e que o ângulo ACB mede 65°, o comprimento total dos cabos subterrâneos é aproximadamente:

Use π ≈ 3,14

Durante a construção de um moderno complexo empresarial, o arquiteto responsável precisa verificar se a fachada de vidro de um dos edifícios está sendo executada conforme o projeto. O edifício possui uma parede lateral completamente vertical de 18 metros de altura, e em sua base foi instalado um painel publicitário retangular de 3 metros de altura.

Para realizar a inspeção visual, o arquiteto se posiciona em um ponto no chão, a uma distância horizontal de 24 metros da base do edifício. Desse ponto de observação, ele consegue enxergar tanto a base quanto o topo da parede do edifício, formando um ângulo de visão que precisa ser calculado para determinar se a perspectiva está adequada para a análise da fachada.

Considerando que o arquiteto está posicionado a 24 metros de distância horizontal da base do edifício, que a parede tem 18 metros de altura total e que há um painel de 3 metros na base (que deve ser desconsiderado), a tangente do ângulo sob o qual o arquiteto visualiza a extensão vertical útil do edifício é:

Uma empresa de agronegócios utiliza drones equipados com câmeras de alta resolução para monitorar suas plantações e detectar pragas ou áreas que necessitam de irrigação. Durante uma operação de mapeamento, um drone decola verticalmente a partir do ponto A, localizado na borda de um campo retangular.

O piloto programa a seguinte rota: o drone sobe 10 metros verticalmente até o ponto C, onde consegue avistar um marco de referência B, situado a 50 metros de distância horizontal do ponto de decolagem A, sob um certo ângulo de depressão.

Para otimizar o mapeamento da área, o drone continua subindo até uma segunda posição D, onde avista o mesmo marco B. Os ângulos ABC e CBD possuem a mesma medida.

A altura vertical percorrida pelo drone de C até D foi de